Practice makes perfect
[R] 척도별 기술 통계량 구하기 본문
척도
- 측정을 목적으로 일정한 규칙에 따라 질적인 측정 대상에 적용할 수 있도록 만들어진 계량적 도구. 즉 측정 도구.
- 변수에 값을 부여하는 방법
- 변수 측정 단위(응답자가 선택핛 수 있는 질문 항목)
연속형 변수 : 양적인 크기를 가지는 변수 (키) - > 등간척도, 비율척도
범주형 변수 : 크기를 가지지 않는 변수 (성별) -> 명목척도, 서열 척도
- 데이터 가져오기
data <-read.csv("C:/workspaces/R/data/descriptive.csv",header = T)
View(data)
위 데이터를 사용하여 살펴보도록 하겠습니다.
- 데이터 정보 확인
dim(data) 출력값 : 300 8 - 차원보기
length(data) 출력값 : 8 (컬럼 수)
length(data$survey) 출력값 : 300(데이터 수)
str(data) 출력값 : 'data.frame': 300 obs. of 8 variables: + 컬럼의 이름 + 자료형 출력
str(data$survey) 출력값 int [1:300] 1 2 1 4 3 3 NA NA NA 1 ...
1. 명목 척도
: 단순히 속성을 분류핛 목적으로 명목상 숫자를 부여하는 척도, 연산 불가능한 변수
length(data$gender) 출력값 300
summary(data$gender)
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 1.00 1.00 1.42 2.00 5.00
table(data$gender) == 각 성별 빈도 수 - outlier(이상치) -> 0,5
- 출력값 -
0 1 2 5
2 173 124 1
- 이상치 제거
data <- subset(data, data$gender==1 | data$gender ==2) # 성별 outlier 제거
x<- table(data$gender) # 성별에 대한 빈도수 저장
x
- 출력값 -
1 2
173 124
- 시각화 + 구성비율 계산
구성비율 계산
prop.table(x) # 비율계산 : 0 < x < 1 사이의 값
-출력값-
1 2
0.5824916 0.4175084
y <- prop.table(x)
round(y*100,2) # 백분율 적용(소수점 2자리)
-출력값-
1 2
58.25 41.75
barplot(x) # 범주형(명목/서열 척도) 시각화 -> 막대 차트 
2. 서열 척도
: 순서관계를 밝혀주는 척도(연산 불가능핚 변수) - 설문의 종류에 따라서 달라짐 (선호도)
- 데이터 정보
length(data$level) 출력값 : [1] 297 -- 학력수준 - 서열 (크기적인 개념 포함)
summary(data$level) # 명목척도와 함께 의미 없음
table(data$level) # 빈도분석 - 의미있음
- 출력값 -
1 2 3
115 99 70
- 구성비율 계산 + 시각화
구성비율 계산
x1 <- table(data$level) # 각 학력수준에 빈도수 저장.
y <- prop.table(x1)
round(y*100,2) # 백분율 적용(소주점 2자리)
- 출력값 -
1 2 3
40.49 34.86 24.65
학력 수준(level) 변수의 빈도 수 시각화
barplot(x1) # 명목/ 서열 척도 -> 막대차트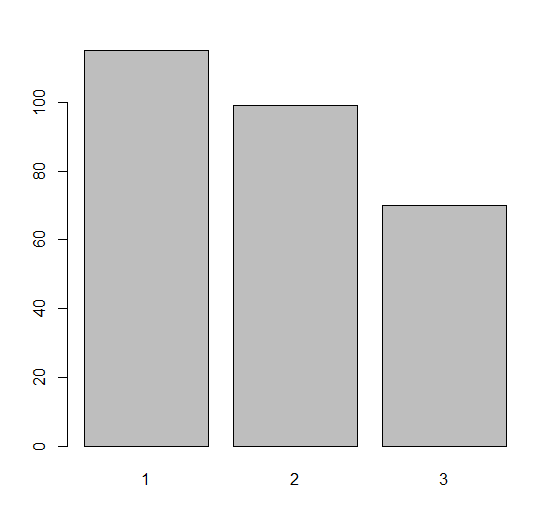
3. 등간척도
: 측정대상의 속성에 대한 각 수준 간의 간격이 동일한 척도, 균일한 분포를 가지면서 연산이 가능
(수치로서의 개념 존재)
- 만족도(survey) 변수
survey <- data$survey
survey
summary(survey) - 만족도(5점척도)인 경우 의미 있음 -> 평균간 : 2.605
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
1.000 2.000 3.000 2.605 3.000 5.000 112
NA의 값이 112개나 되기 때문에 배제해 버리면 sample의 데이터가 많이 사라지므로 결과가 이상하게 출력될 수 있습니다.
- 빈도수 + 시각화
x1 <- table(survey) # 빈도수
x1
- 출력값 -
1 2 3 4 5
20 72 61 25 7
hist(survey) # 등간척도 시각화(연속형 변수)
pie(x1) # 분포도 특징 시각화
- hsit
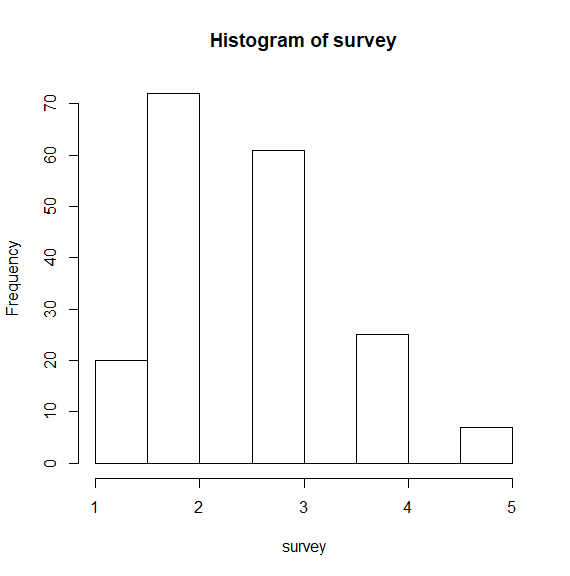
- pie

4. 비율척도
: 척도의 수가 등간 , 사측 연산 가능
등간척도와 비율척도의 차이는 절대 원점(0)의 의미 입니다.
- 등간척도는 절대원점(0)을 가지고 있지 않음(의미 없음)
- 비율척도는 절대원점(0)을 가지고 있는 척도(0을 기준으로 한 수치)
생황비(cost) 변수 대상 요약 통계량 구하기
length(data$cost) # 297 (레코드 개수)
summary(data$cost) # 요약통계량 - 의미 있음(mean) / Mean = 8.784 , Median = 5.4
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
-457.200 4.400 5.400 8.784 6.300 675.000 30
plot(data$cost) # 분포도 확인 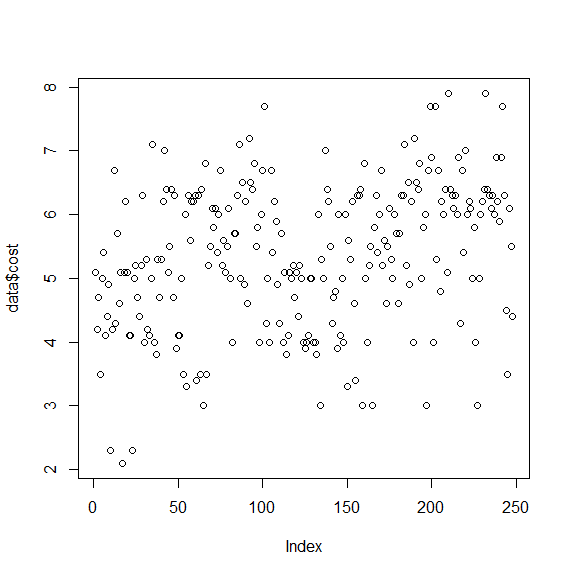
데이터 정제(이상치 제거)
data <- subset(data, data$cost>=2 & data$cost <= 10) # 총점기준
plot(data$cost)
x <- data$cost
mean(x) 출력값 : 5.354032
평균이 극단치에 영향을 받는 경우 = 중위수(median) 대체
median(x) 출력값 : 5.4
● 대표값 구하기
생활비(cost) 변수 대상 대표값 구하기
mean(x) 출력값 : 5.354032
median(x) 중위값 : 5.4
sort(x) # 오름차순(default) = decreasing = F
sort(x, decreasing = T) # 내림차순

생활비(cost) 변수 대상 사분위수 구하기
- quantile() : 분위별 결과 출력
quantile(x, 1/4) # 1분위
-출력값-
25%
4.6
quantile(x, 2/4) # 2분위
-출력값-
50%
5.4
quantile(x, 3/4) # 3분위
-출력값-
75%
6.2
quantile(x, 4/4) # 4분위
-출력값-
100%
7.9
● 산포도 구하기
생활비(cost) 변수 대상 산포도 구하기
var(x) # 분산
출력값: [1] 1.296826
sd(x) # 표준편차
출력값 [1] 1.138783
# 분산 -> 표준편차
sqrt(var(x)) : 출력값 : [1] 110.3872
# 표준편차 -> 분산
sd(x) ** 2 : 출력값 : [1] 12185.33
● 빈도 분석
생활비(cost) 변수의 빈도분석과 시각화
table(data$cost)
hist(data$cost) # 히스토그램 시각화
plot(data$cost) # 산점도 시각화
hist(data$cost)

plot(data$cost)

연속형 변수 범주화
data$cost2[data$cost >= 2 & data$cost < 4] <- 1
data$cost2[data$cost >= 4 & data$cost < 7] <- 2
data$cost2[data$cost >= 7] <- 3
x <- table(data$cost2)
barplot(x)
pie(x)barplot(x)

pie(x)

5. 비대칭도 구하기
- pakage 설치 및 데이터 정리
install.packages("moments")
library(moments)
cost <- data$cost
cost
왜도 - 평균을 중심으로 기울어진 정도. < skewness() >
skewness(cost) 출력값 : [1] -0.297234
첨도 - 표준 정규 분포와 비교하여 얼마나 뽀족한가 측정 지표 < kurtosis() >
kurtosis(cost) 출력값 : [1] 2.674163
hist(cost) - 기본 히스토그램

hist(cost, freq = F) - 히스토그램 확률밀도/표준 정규 분포 곡선
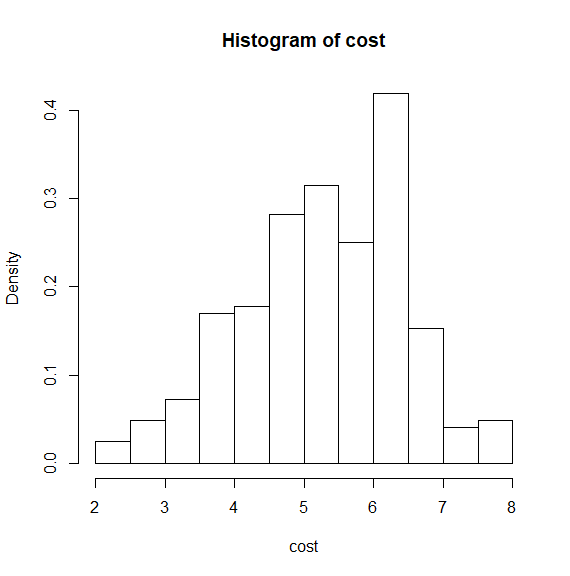
lines(density(cost), col='blue') - 히스토그램 확률밀도/표준 정규 분포 곡선

표준정규분포 곡선
x <- seq(0, 8, 0.1)
curve(dnorm(x, mean(cost), sd(cost)), col='red', add = T)
6. 패키지 기술 이용 통계량 구하기

위 데이터를 활용하여 살펴보겠습니다.
① Hmisc 패키지 이용
- Hmisc 패키지 설치
install.packages("Hmisc")
library(Hmisc)
전체 변수 대상 기술통계량 제공 - 빈도와 비율 데이터 일괄 수행(각 컬럼별로 계산해서 결과값을 출력)
describe(data) 
개별 변수 기술 통계량
describe(data$gender) # 특정 변수(명목) 기술통계량-범주/빈도수/비율 제공.

describe(data$age) # 특정 변수(비율) 기술통계량 - lowest / highest

② prettyR 패키지 이용
- prettyR 패키지
install.packages("prettyR")
library(prettyR)
- 전체 변수 대상
freq(data) # 각 변수별 : 빈도, 결측치, 백분율, 특징-소수점 제공 
- 개별 변수 대상
freq(data$gender) # 빈도, 결측치, 백분율
'빅데이터 > R' 카테고리의 다른 글
| [R] 카이제곱(chi-square 검정) (1) | 2020.07.15 |
|---|---|
| [R] 교차분석(Cross Table Analyze) (0) | 2020.07.14 |
| [R] 평균, 분산, 표준변차 (0) | 2020.07.13 |
| [R] 텍스트 마이닝 분석 - 실시간 뉴스 수집과 분석 (1) | 2020.07.13 |
| [R] 통계 분석 절차 (0) | 2020.07.10 |



