Practice makes perfect
[R] 추정(estimation) + (표본크기 결정) 본문
추정(estimation)
: 표본을 통해서 모집단을 확률적으로 추측
1) 점 추정 : 제시된 한 개의 값과 검정통계량(표본을 통해 계산된 통계량)을 직접 비교하여 가설 기각 유무를 결정
ex) 우리 나라 중학교 2학년 남학생 평균키는 165.2cm로 추정 (거의 불가능)
2) 구간 추정 : 신뢰구간과 검정통계량을 비교하여 가설 기각유무 결정 - 일반적으로 많이 사용
신뢰구간 : 오차범위에 의해서 결정된 하한값과 상한값의 범위
ex) 우리 나라 중학교 2학년 남학생 평균키는 164.5 ~ 165.5cm로 추정
용어 정의.
- (가설) 검정(hypotheses testing) : 유의 수준과 표본의 검정통계량을 비교하여 통계적 가설의 진위를 입증
- 검정통계량 : 표본에 의해서 계산된 통계량(표본평균, 표본표준편차)
- 모수 : 모집단에 의해서 나온 통계량(모평균, 모표준편차)
예제) 우리나라 중학교 2학년 남학생 평균 신장 표본 조사
- 전체 표본 크기(N) : 10,000명
- 표본평균(X) : 165.1 cm
- 표본 표준편차(S) : 2 cm
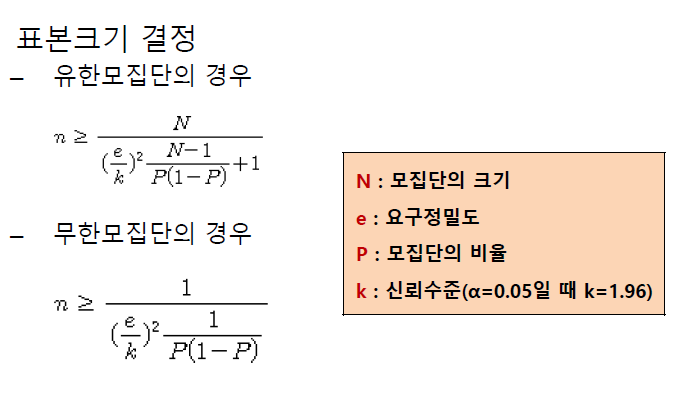
표본크기 결정
① 요구정밀도 e의 결정 : 허용가능 최대오차(10% 설정)
② 신뢰수준 α의 결정 : 95% 신뢰도(α=0.05 설정)
– 95% 신뢰도 → α=0.05 → k = 1.96
– 90% 신뢰도 → α=0.1 → k = 1.65
– 99% 신뢰도 → α=0.01 → k = 2.58
③모집단 비율 P 예측 : 예비조사 결과나 기졲의 설문조사 결과를 기초로 P값 예측
(예측 불가능한 경우 P(찬성률) 50% 설정)
④수식 계산 : 유한 또는 무한모집단의 특성을 고려 해당 수식 적용
- 모평균 신뢰수준 95%의 신뢰구간(하한값과 상한값) 구하기
N <- 10000 # 표본크기
X <- 165.1 # 표본평균
S <- 2 # 표본 표준편차
low <- X - 1.96 * S / sqrt(N) # 신뢰구간 하한값 # sqrt() : 제곱근 계산
high <- X + 1.96 * S / sqrt(N) # 신뢰구간 상한값
low; high # 165.0608 ~ 165.1392
-출력값-
[1] 165.0608
[1] 165.1392해석 : 신뢰수준 95%는 신뢰구간이 모수를 포함할 확률을 의미하고, 신뢰구간은 오차범위에 의해서 결정된 하한값~상한값을 의미합니다.
- 신뢰구간으로 표본오차 구하기
low - X 출력값 : -0.0392 = 신뢰구간 하한값(165.0608) - 표본 평균 (x= 165.1)
high -X 출력값 : 0.0392 = 신뢰구간 상한값(065.1392) - 표본 평균 (x= 165.1)
(low - X) * 100 # -3.92
(high - X) * 100 # 3.92최종 해석 : 우리나라 중학교 2학년 남학생 평균 신장이 95% 신뢰 수준에서 표본오차 -3.92~3.92 범위에서 165.1cm로 조사가 되었다면, 실제 평균키는 165.0608cm ~ 165.1392cm 사이에 나타날 수 있다는 것을 의미합니다.
- 표본 크기 결정 예제
A전기 회사의 사원수가 5,000명인 경우 요구정밀도 10%, 신뢰수준 95% 일 때 표본의 크기는 얼마인가?

N: 모집단 크기, e: 요구정밀도, P: 모집단 비율, k: 신뢰수준

'빅데이터 > R' 카테고리의 다른 글
| [R] 집단 간 차이 분석 (part_2 두 집단 분석) (0) | 2020.07.15 |
|---|---|
| [R] 집단 간 차이 분석 (part_1 단일 집단 분석) (0) | 2020.07.15 |
| [R] 카이제곱(chi-square 검정) (1) | 2020.07.15 |
| [R] 교차분석(Cross Table Analyze) (0) | 2020.07.14 |
| [R] 척도별 기술 통계량 구하기 (0) | 2020.07.14 |




