Practice makes perfect
[R] 집단 간 차이 분석 (part_1 단일 집단 분석) 본문
단일 집단 검정
: 한 개의 집단과 기존 집단과의 비율/평균 차이 검정
1. 단일 집단 비율 검정
- 단일 집단의 비율이 어떤 특정한 값과 같은지를 검정하는 방법
- 기술통계량으로 빈도 수에 대한 비율에 의미
- 단일 집단의 비율이 어떤 특정한 값과 같은지를 검정하는 방법(검정 방법 중에서 가장 간단)
방법: 1개 집단의 비율과 기존 집단과의 비율 차이 분석
작업절차
1. 실습 데이터 가져오기
2. 빈도수와 비율 계산
3. binom.test() 이용
분석 절차
실습파일 가져오기 -> 데이터 전처리 -> 기술통계량(빈도분석) -> binom.test() -> 검정통계량 분석
<연구가설>
연구가설(H1) : 기존2014년도 고객 불만율과 2015년도 CS교육후 불만율에 차이가 있다.
귀무가설(H0) : 기존2014년도 고객 불만율과 2015년도 CS교육후 불만율에 차이가 없다
<연구환경>
2014년도 114 전화번호 안내 고객을 대상으로 불만을 갖는 고객은 20% 였다. 이를 개선하기 위해서 2015년도 CS교육을 실시한 후 150명 고객을 대상으로 조사한 결과 14명이 불만을 갖고 있었다. 기존20% 보다 불만율이 낮아졌다고 할 수 있는가?
대상파일: c:/workspaces/Rwork/data/one_sample.csv
해당변수 : survey(만족도)
변수척도 : 명목척도(y/n)
가정 : 기존 불만율과 CS교육후 불만율 분석
1단계 실습 파일 가져오기
data <- read.csv("C:/workspaces/R/data/one_sample.csv", header = T)
head(data)
- 출력값 -
no gender survey time
1 1 2 1 5.1
2 2 2 0 5.2
3 3 2 1 4.7
4 4 2 1 4.8
5 5 2 1 5.0
6 6 2 1 5.4
View(data)
2단계 데이터 전처리 (빈도수와 비율 계산)
x <- data$survey
x
summary(x) # 결측치 확인
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000 1.0000 1.0000 0.9067 1.0000 1.0000
length(x) 출력값 : [1] 150
table(x) # 빈도수(0:불만족(14), 1:만족(136))
x
- 출력값 -
0 1
14 136
3단계 기술통계량(빈도분석) - (패키지 이용 빈도수와 비율계산)
library(prettyR) # freq() 함수 사용
freq(x)
- 출력값 -
Frequencies for x
1 0 NA
136 14 0
% 90.7 9.3 0
%!NA 90.7 9.3
-- 이항분포 (만족율 기준) 비율검정 --
1) 양측 검정 (있다 or 없다)
binom.test(c(136, 14), p=0.8) # 기존 80% 만족율 기준 검증 실시 
p-value = 0.0006735 < 0.05 보다 작다 -> 귀무가설 기각, 연구가설 채택(유의확률 값으로 결과 도출)
해설: 기존만족율(80%)과 차이가 있다. -> 연구가설채택 - 연구가설(H1) : 기존 2014년도 고객불만율과 2015년도 CS교육 후 불만율에 차이가 있다. 라는 결과를 도출합니다.
주의 사항) 차이가 없으면 문제가 없지만, 차이가 있게 되면 그 차이가 긍적적인지 부정적인지 판단할 수 없습니다.
2) 방향성을 갖는 단측 가설 검정 (방향성(긍정/부정)) - (유의확률 값이 유일수준 보다 작으면 채택)
- alternative = "greater"
binom.test(c(136, 14), p=0.8, alternative = "greater", conf.level = 0.95) # p-value = 0.0003179
# greater : ~보다 크다(방향성)

전체 비율이 80% 보다 큰가? 80% 보다 크다.
p-value = 0.0003179 < 0.05 : 작으므로 채택(긍정적 차이를 얻어낸다)
- alternative = "less"
binom.test(c(136, 14), p=0.8, alternative = "less", conf.level = 0.95) # p-value = 0.9999
# less : 작다(방향성)
p-value = 0.9999 > 0.05 : 크므로 기각된다. - 사용하지 않는다.
결론 : 긍정적인 차이를 낸다.
-- 이항분포 (불만족 기준) 비율검정 --
1) 양측검정
binom.test(c(14, 136), p=0.2) # 기존 20% 불만족율 기준 검증 실시 p-value = 0.0006735 < 0.05 보다 작다 -> 귀무가설 기각, 연구가설 채택(유의확률 값으로 결과 도출)
해설: 기존만족율(80%)과 차이가 있다. -> 연구가설채택 - 연구가설(H1) : 기존 2014년도 고객불만율과 2015년도 CS교육 후 불만율에 차이가 있다. 라는 결과를 도출합니다.
< 양측검정은 불만족과 만족의 결과는 같습니다 >
2) 방향성을 갖는 단측 가설 검정 (유의확률 값이 유일수준 보다 작으면 채택)
- alternative = "greater"
binom.test(c(14, 136), p=0.2, alternative = "greater", conf.level = 0.95)p-value = 0.9999 - 기각 ( 0.9999 > 0.05 )
- alternative = "less"
binom.test(c(14, 136), p=0.2, alternative = "less", conf.level = 0.95)p-value = 0.0003179 - 채택 ( 0.0003179 < 0.05 )
결과 : 불만족의 부정적 차이 이므로 - 긍정적 차이를 나타낸다.
2 단일집단 평균검정(단일표본 T검정)
: 단일집단의 평균이 어떤 특정한 집단의 평균과 차이가 있는지를 검정하는 방법으로, 기술통계량으로 표본평균에 의미
방법: 두 집단 간 평균 차이에 관한 분석
작업절차
1. 실습 파일 가져오기
2. 두 집단 subset 작성(데이터정제,전처리)
3. 두 집단간 동질성 검증(정규 분포 검정)
-> var.test()
4. 두집단 평균 차이 검정
-> 정규분포를 따를 때 = t.test() or 정규분포를 따르지 않을 때 = wilcow.test()
분석절차

<가설설정>
- 연구가설(H1) : 국내에서 생산된 노트북과 A회사에서 생산된 노트북의 평균 사용 시간에 차이가 있다.
- 귀무가설(H0) : 국내에서 생산된 노트북과 A회사에서 생산된 노트북의 평균 사용 시간에 차이가 없다.
<연구환경>
IT교육센터에서 PT를 이용한 프레젠테이션 교육방법과 실시간 코딩 교육 방법을 적용하여 1개월 동안 교육 받은 교육생 각150명을 대상으로 실기시험을 실시하였다. 두집단간 실기시험의 평균에 차이가 있는가 검정한다
해당변수: method(명목척도), score(비율척도)
대상변수: 교육방법, 시험성적
모형(모델) : 교육방법(A/B) -> 시험성적(비율-성적)
1단계 파일 가져오기
data <- read.csv("C:/workspaces/R/data/one_sample.csv", header = T)
head(data)
- 출력값 -
no gender survey time
1 1 2 1 5.1
2 2 2 0 5.2
3 3 2 1 4.7
4 4 2 1 4.8
5 5 2 1 5.0
6 6 2 1 5.4
str(data)
- 출력값 -
'data.frame': 150 obs. of 4 variables:
$ no : int 1 2 3 4 5 6 7 8 9 10 ...
$ gender: int 2 2 2 2 2 2 2 2 2 1 ...
$ survey: int 1 0 1 1 1 1 1 1 0 1 ...
$ time : num 5.1 5.2 4.7 4.8 5 5.4 NA 5 4.4 4.9 ...
x <- data$time
head(x) 출력값 : [1] 5.1 5.2 4.7 4.8 5.0 5.4
2단계 데이터 전처리 (데이터 분포/결측치 제거)
summary(x) # NA's -> 41
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
3.000 5.000 5.500 5.557 6.200 7.900 41
mean(x) 출력값 : [1] NA
3단계 데이터 정제
mean(x, na.rm=T) # NA 제외 평균(방법1) 출력값 : [1] 5.556881
x1 <- na.omit(x) # NA 제외(방법2)
mean(x1) 출력값 : [1] 5.556881
4단계 정규분포 검정
- 귀무가설(H0) : x의 데이터 분포는 정규분포
- shapior.test(정규분포 검정) 값이 인계치보다 높으면 따른다고 볼 수 있습니다.
shapiro.test(x1)

정규분포 검정 함수(p-value = 0.7242), 표본이 정규 분포로부터 추출된 것인지 테스트하기 위한 함수로, 이때 귀무가설은 주어진 데이터가 정규 분포로부터의 표본이라고 합니다.
p-value > α(알파) : 정규분포로 본다.(정규분포를 따른다)
5단계 정규분포 시각화
hist(x1)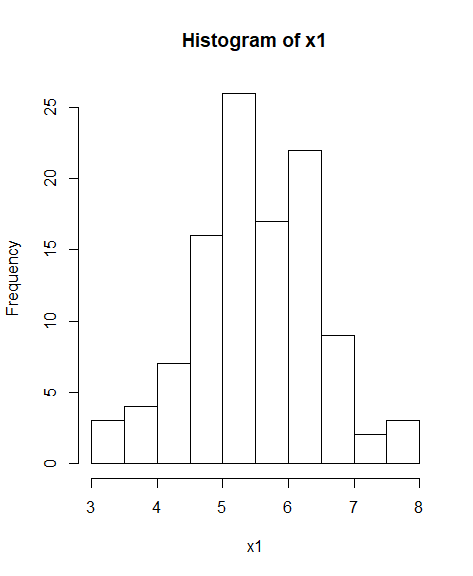
qqline(x1, lty=1, col='blue')
stats 패키지에서 정규성 검정을 위해서 제공되는 시각화 함수

파란줄 : 정규분포도를 따랐을 때 - 분포도 / 정규분포도를 따르고 있음을 시각적으로 확인 할 수 있습니다.
6단계 평균차이 검정
T-test(T-검정) : 모집단에서 추출한 표본 데이터의 분포형태가 정규분포일 때 수행
- 양측검정: x1 객체와 기존 모집단의 평균 5.2시간 비교
t.test(x1, mu=5.2, alternative = "two.side", conf.level = 0.95) mu= "기준치 값"
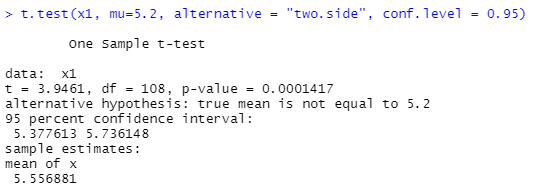
p-value = 0.0001417 < 0.05 = 연구가설 채택 : 연구가설(H1):국내에서 생산된 노트북과 A회사에서 생산된 노트북의 평균 사용 시간에 차이가 있다. 라는 결과를 도출합니다.
- 방향성을 갖는 단측가설 검정 (유의확률 값이 유일수준 보다 작으면 채택)
t.test(x1, mu=5.2, alternative = "greater", conf.level = 0.95)
p-value = 7.083e-05 < 0.05 : 5.2의 시간보다 평균시간이 더 크다는 결과를 도출할 수 있습니다.
7.083e-05 (=0.000007083)
'빅데이터 > R' 카테고리의 다른 글
| [R] 집단 간 차이 분석 (part_3 세 집단 분석(분산 분석)) (0) | 2020.07.16 |
|---|---|
| [R] 집단 간 차이 분석 (part_2 두 집단 분석) (0) | 2020.07.15 |
| [R] 추정(estimation) + (표본크기 결정) (0) | 2020.07.15 |
| [R] 카이제곱(chi-square 검정) (1) | 2020.07.15 |
| [R] 교차분석(Cross Table Analyze) (0) | 2020.07.14 |




