Practice makes perfect
[R] 집단 간 차이 분석 (part_3 세 집단 분석(분산 분석)) 본문
세 집단 평균 검정(분산 분석)
방법: 세집단(이상)간 평균 차이에 관한분석
작업절차
1. 파일 가져오기
2. 데이터 정제/전처리 - NA, outline 제거
3. 세집단 subset 작성
-> 코딩 변경
-> 기술 통계량(빈도수)
-> 교차표 작성
4. 세 집단 동질성 검정 : bartlett.test()
5. 분산 검정 : aov() or kruskal.test()
6. 사후 검정 : TukeyHSD()
분산 절차

<연구 가설>
- 연구 가설(H1) : 교육방법에 따른 세 집단간 실기 시험의 평균에 차이가 있다.
- 귀무 가설(H0) : 교육방법에 따른 세 집단간 실기 시험의 평균에 차이가 없다.
<연구환경>
세 가지 교육방법을 적용하여 1개월 동안 교육 받은 교육생 각 50명씩을 대상으로 실기시험을 실시 하였다. 세 집단간 실기 시험의 평균에 차이가 있는가 검정 한다.
해당변수 : method(명목척도), score(비율척도)
대상변수 : 교육방법, 시험성적
모형(모델) : 교육방법(A/B) -> 시험성적(비율-성적)
1) 세 집단 subset 작성과 기술 통계량 계산
1단계 파일 가져오기
data <- read.csv("C:/workspaces/R/data/three_sample.csv", header = T)
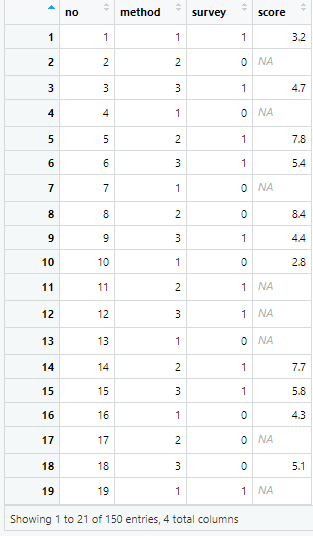
head(data)
- 출력값 -
no method survey score
1 1 1 1 3.2
2 2 2 0 NA
3 3 3 1 4.7
4 4 1 0 NA
5 5 2 1 7.8
6 6 3 1 5.4
str(data)
- 출력값 -
'data.frame': 150 obs. of 4 variables:
$ no : int 1 2 3 4 5 6 7 8 9 10 ...
$ method: int 1 2 3 1 2 3 1 2 3 1 ...
$ survey: int 1 0 1 0 1 1 0 0 1 0 ...
$ score : num 3.2 NA 4.7 NA 7.8 5.4 NA 8.4 4.4 2.8 ...
summary(data)
- 출력값 -
no method survey score
Min. : 1.00 Min. :1 Min. :0.0000 Min. : 2.00
1st Qu.: 38.25 1st Qu.:1 1st Qu.:0.0000 1st Qu.: 4.35
Median : 75.50 Median :2 Median :1.0000 Median : 5.80
Mean : 75.50 Mean :2 Mean :0.7333 Mean : 14.45
3rd Qu.:112.75 3rd Qu.:3 3rd Qu.:1.0000 3rd Qu.: 6.50
Max. :150.00 Max. :3 Max. :1.0000 Max. :478.00
NA's :59
View(data)
※ 150개의 레코드, 50개씩 3가지 그룹
2단계 데이터 전처리 (데이터 정제)
method <- data$method # 공부방법
survey <- data$survey # 만족도 (만족 : 1 , 불만족 : 0) : 비율의 차이점 을 검정(빈도수)
method; survey

3단계 기술통계량 (빈도분석)
table(method, useNA = "ifany") - NA 제외
- 출력값 -
method -> 3그룹 모두 관찰치 각 50개
1 2 3
50 50 50
table(method, survey, useNA = "ifany") - NA 제외
- 출력값 -
survey (만족 : 1 , 불만족 : 0) : 비율의 차이점 을 검정(빈도수)
method 0 1
1 16 34
2 13 37
3 11 39useNA = "ifany" : 결측치 존재시 display
2) 세 집단 비율 차이 검정
- 양측 검정
prop.test(c(34,37,39), c(50,50,50)) - 입력 값에 따라 변경
prop.test(c(34,37,39), c(50,50,50), alternative = "two.sided", conf.level = 0.95)

p-value = 0.5232(유의확률) > 0.05(유의수준) -> 귀무가설 채택 : 교육방법에 따른 세 집단간 실기 시험의 평균에 차이가 없다.
- 귀무가설이 채택 되었기 때문에 단측 검정이 필요하지 않습니다.
- 위의 결과를 가지고는 주장하고 싶은바의 근거로 제시할 수 없습니다.
2. 분산분석(F 검정, ANOVA Analysis)
: 세 집단 이상의 평균 차이 검정
1) 데이터 전처리
1단계 파일 가져오기, 전처리
data <- read.csv("C:/workspaces/Rwork/data/three_sample.csv", header = T)
summary(data) - NA : 59 개
- 출력값 -
no method survey score
Min. : 1.00 Min. :1 Min. :0.0000 Min. : 2.00
1st Qu.: 38.25 1st Qu.:1 1st Qu.:0.0000 1st Qu.: 4.35
Median : 75.50 Median :2 Median :1.0000 Median : 5.80
Mean : 75.50 Mean :2 Mean :0.7333 Mean : 14.45
3rd Qu.:112.75 3rd Qu.:3 3rd Qu.:1.0000 3rd Qu.: 6.50
Max. :150.00 Max. :3 Max. :1.0000 Max. :478.00
NA's :59
data <- subset(data, !is.na(score), c(method, score)) # NA 생략
head(data)
- 출력값 -
method score
1 1 3.2
3 3 4.7
5 2 7.8
6 3 5.4
8 2 8.4
9 3 4.4
2단계 차트 이용 - outlier 보기(데이터 분포 현황 분석)
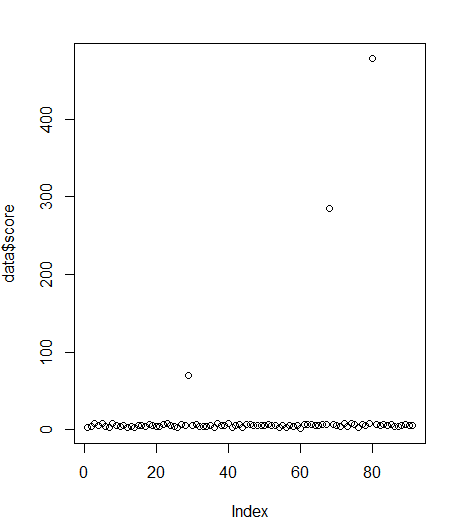
plot(data$score) # 차트로 outlier 확인 : 50이상과 음수값
barplot(data$score) # 바 차트
mean(data$score) 출력값 : [1] 14.44725plot(data$score)
barplot(data$score)
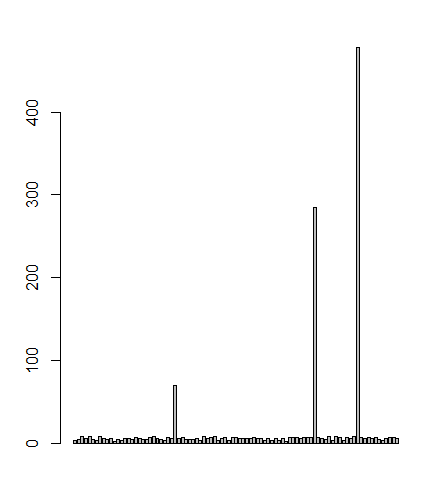
3개의 데이터가 문제를 가지고 있는 것처럼 보입니다.
3단계 outlier 제거 - 평균(14.44725)
length(data$score) 출력값 : [1] 91
data2 <- subset(data, score <= 14) - 14이상 제거
length(data2$score) 출력값 : [1] 88 (3개 필터링)
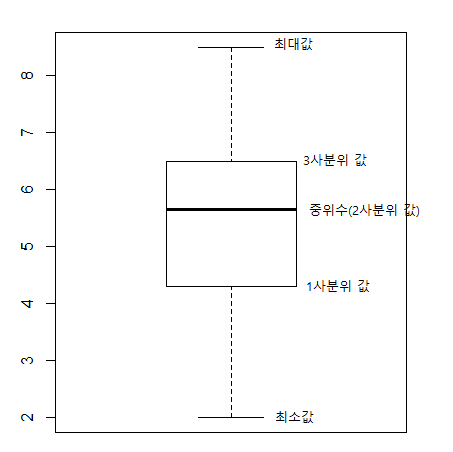
4단계 정제된 데이터 보기
x <- data2$score
summary(x)
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.000 4.300 5.650 5.474 6.500 8.500
boxplot(x)
2) 세 집단 subset 작성과 기술통계량
1단계 세 집단 subset 작성
data2$method2[data2$method == 1] <- "방법1"
data2$method2[data2$method == 2] <- "방법2"
data2$method2[data2$method == 3] <- "방법3"
View(data2)
2단계 교육 방법별 빈도수
x <- table(data2$method2)
x
- 출력값 -
방법1 방법2 방법3
31 27 30
3단계 교육방법에 따른 시험성적 평균 구하기
y <- tapply(data2$score, data2$method2, mean)
y
- 출력값 -
방법1 방법2 방법3
4.187097 6.800000 5.610000 tapply : 두개 이상의 변수를 비교하면서 3번째 넣은 기능을 수행 (base패키지에서 제공)
4단계 교육방법과 시험성적으로 데이터프레임 생성
df <- data.frame(교육방법 = x, 성적 = y)
df
- 출력값 -
교육방법.Var1 교육방법.Freq 성적
방법1 방법1 31 4.187097
방법2 방법2 27 6.800000
방법3 방법3 30 5.610000
3) 세 집단 간 동질성 검정
bartlett.test(score ~ method2, data = data2) bartlett.test(종속변수(y축) ~ 독립변수(x축) , data)
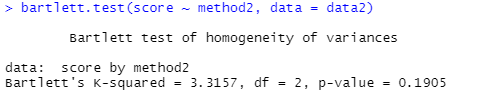
p-value = 0.1905 > 0.05 : 귀무가설 채택 - 동질성ok
4) 분산 분석(세 집단 간 평균 차이 검정) , F 검정(분석), ANOVA 검정(분석)
result <- aov(score ~ method2, data = data2)
result -- 주의)검정에 필요한 값을 얻지 못합니다.
- 출력값 -
Call:
aov(formula = score ~ method2, data = data2)
Terms:
method2 Residuals
Sum of Squares 99.36805 96.90184
Deg. of Freedom 2 85
Residual standard error: 1.067718
Estimated effects may be unbalanced
names(result) - 컬럼의 이름 반환
- 출력값 -
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "contrasts" "xlevels" "call" "terms"
[13] "model"
summary(result) aov(종속변수(y축) ~ 독립변수(x축) , data)

p-value=9.39e-14 < 0.05 귀무가설 기각
5) 사후 검점
집단간 차이 상세보기 --> A!=B!=C, A==B!=C, A!=B==C
TukeyHSD(result) 
교육방법 간 비교 --> p 값 tapply 차이 검정 ) --> 4.187097 6.800000 5.610000
6) 사후 검정 시각화
plot(TukeyHSD (result))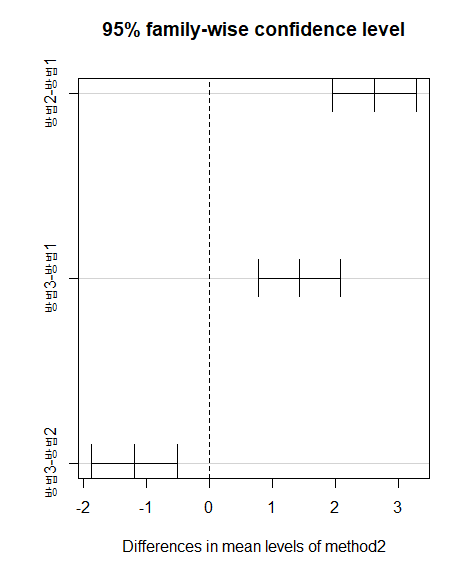
해석 ) A, B, C 집단간 모두 차이 존재
최종 결과 : 유의수준 0.05 에서 귀무가설이 기각되었다 . 따라서 교육방법에 따른 세 집단 간 실기시험의 평균에 차이가 있는 것으로 나타났다 . 또한 사후검정 방법인 Tukey 분석을 실시한 결과 '방법2 - 방법1’ 의 평균 점수의 차이가 가장 높은 것으로 나타났다.
'빅데이터 > R' 카테고리의 다른 글
| [R] 상관관계 분석(Correlation Analysis) (0) | 2020.07.17 |
|---|---|
| [R] 요인분석(Factor Analysis) (1) | 2020.07.16 |
| [R] 집단 간 차이 분석 (part_2 두 집단 분석) (0) | 2020.07.15 |
| [R] 집단 간 차이 분석 (part_1 단일 집단 분석) (0) | 2020.07.15 |
| [R] 추정(estimation) + (표본크기 결정) (0) | 2020.07.15 |




