Practice makes perfect
[R] 요인분석(Factor Analysis) 본문
요인분석(Factor Analysis) - 예측분석
: 여러개의 서로 관련이 있는 변수들로 측정된 자료에서 그 변수들을 설명할 수 있는 새로운 공통변수를 파악하는 통계적 분석방법입니다. 유사성을 띈 데이터의 축약을 목적으로 하는 분석방법이라고 할 수 있습니다.
● 요인분석의 특징
1) 다수의 변수들을 대상으로 변수들 간의 관계 분석(타당성 분석)
2) 공통 차원으로 축약하는 통계기법(변수 축소) - 데이터 축소
- 유사성을 가진 데이터들을 하나로 묶음.
● 요인분석의 종류(개입의 여부로 나눔)
1) 탐색적 요인분석 : 요인분석을 할 때 사전에 어떤 변수들끼리 묶어야 한다는 전제를 두지 않고 분석하는 방법(개입X)
- 변수 압축이 목적(주성분분석, 주요인분석, 최대우도요인분석 ...)
2) 확인적 요인분석 : 요인분석을 할 때 사전에 묶여질 것으로 기대되는 항목끼리 묶여지는지를 분석하는 방법(개입O)
- 어떤 가설이나 모델의 검증이 목적
● 요인분석의 방법
1) 변수간의 상관행렬로부터 공통요인을 도출
2) 도출된 공통요인을 이용해서 변수간의 상관관계를 설명
3) 요인부하량(factor loading)은 ±0.3 이상이면 유의하다고 봄.
● 요인의 수와 유의성 판단 기준
- 상관 계수 행렬 R의 고유값이 1이상인 경우 채택하며, 요인의 유의성은 다음의 기준을 따른다.
- 수학적 근거 보다는 통상적으로 개체수 n>= 50인 경우 절대값 기준으로
요인부하값 > 0.3 : 유의함
요인부하값 > 0.4 : 좀 더 유의함
요인부하값 > 0.5 : 아주 유의함
● 요인분석의 목적
1) 자료의 요약 : 변인을 몇 개의 공통된 변인으로 묶음 (주성분 분석과 비슷)
- 같은 개념을 측정하는 변수들이 동일한 요인으로 묶이는지 확인
2) 변인 구조 파악 : 변인들의 상호관계 파악(독립성 등)
3) 불필요한 변인 제거 : 중요도가 떨어진 변수 제거
4) 측정도구 타당성 검증 : 변인들이 동일한 요인으로 묶이는지 여부를 확인 / ex ) 설문의 질문의 타당성
- 회귀분석이나 판별분석의 설명변수 선택
● 전제조건
- 등간척도 or 비율척도, 정규분포, 관찰치 상호독립적/분산 동일
- 하위요인으로 구성되는 데이터 셋이 준비되어 있어야 함.
- 분석에 사용되는 변수는 등간척도나 비율척도이여야 하며, 표본의 크기는 최소 50개 이상이 바람직함 【중심극한정리】
- 요인분석은 상관관계가 높은 변수들끼리 그룹화하는 것이므로 변수들 간의 상관관계가 매우 낮다면(보통 ±3 이하)
그 자료는 요인 분석에 적합하지 않음.
- 변수간에 높은 상관관계가 있어야 함.
- 최초 요인 추출 단계에서 얻은 고유치를 스크리 차트로 표시했을 때 한 군데 이상 꺽이는 곳이 있어야 함.
- 모상관 행렬이 단위 행렬이라는 가설이 기각되어야 함. (KMO and Bartleet's 검정)
● 요인분석 결과에 대한 활용 방안
- 서로 밀접하게 관련된 변수들을 합치거나 중복된 변수를 제거하여 변수를 축소
- 변수들 간의 연관성 또는 공통점 탐색
- 요인점수 계산으로 상관분석, 회귀분석의 설명변수로 이용
* 요인 추가정보
요인
factor 범주형 변수(요인형 변수)에서 가질 수 있는 값을 범주라고 합니다. .
ex) 성별 - 남, 여
- factor의 자료형 = numeric
why : 요인이 가지는 개수를 요인이라는 자료형에서 관리하고 그것을 자료형인 numeric(값이 가질 수 있는 범위) 으로보여줍니다.
ex ) factor의 자료형(=numeric)
gender <- c('man','woman','woman','man','woman')
mode(gender) 출력값 : character
요인형 변환
as.factor() 함수 이용 범주(요인)형 변환
Ngender <- as.factor(gender)
mode(Ngender) 출력값 : "numeric"
대표적인 요인형으로 관리하는 요소 : 명목척도, 서열척도
+ 요인 ) 순서를 부여할 수 있다. ( default = 순서 x (알파벳 순서) )
1. 공통요인으로 변수 정제
- 변수와 데이터프레임 생성
s1 <- c(1, 2, 1, 2, 3, 4, 2, 3, 4, 5) # s1 : 자연과학
s2 <- c(1, 3, 1, 2, 3, 4, 2, 4, 3, 4) # s2 : 물리화학
s3 <- c(2, 3, 2, 3, 2, 3, 5, 3, 4, 2) # s3 : 인문사회
s4 <- c(2, 4, 2, 3, 2, 3, 5, 3, 4, 1) # s4 : 신문방송
s5 <- c(4, 5, 4, 5, 2, 1, 5, 2, 4, 3) # s5 : 응용수학
s6 <- c(4, 3, 4, 4, 2, 1, 5, 2, 4, 2) # s6 : 추론통계
name <-1:10 # 각 과목 문항 이름
subject <- data.frame(s1, s2, s3, s4, s5, s6)
subject
-출력값-
s1 s2 s3 s4 s5 s6
1 1 1 2 2 4 4
2 2 3 3 4 5 3
3 1 1 2 2 4 4
4 2 2 3 3 5 4
5 3 3 2 2 2 2
6 4 4 3 3 1 1
7 2 2 5 5 5 5
8 3 4 3 3 2 2
9 4 3 4 4 4 4
10 5 4 2 1 3 2
str(subject)
- 출력값 -
'data.frame': 10 obs. of 6 variables:
$ s1: num 1 2 1 2 3 4 2 3 4 5
$ s2: num 1 3 1 2 3 4 2 4 3 4
$ s3: num 2 3 2 3 2 3 5 3 4 2
$ s4: num 2 4 2 3 2 3 5 3 4 1
$ s5: num 4 5 4 5 2 1 5 2 4 3
$ s6: num 4 3 4 4 2 1 5 2 4 2
summary(subject)
- 출력값 -
s1 s2 s3 s4 s5 s6
Min. :1.00 Min. :1.00 Min. :2.0 Min. :1.00 Min. :1.00 Min. :1.0
1st Qu.:2.00 1st Qu.:2.00 1st Qu.:2.0 1st Qu.:2.00 1st Qu.:2.25 1st Qu.:2.0
Median :2.50 Median :3.00 Median :3.0 Median :3.00 Median :4.00 Median :3.5
Mean :2.70 Mean :2.70 Mean :2.9 Mean :2.90 Mean :3.50 Mean :3.1
3rd Qu.:3.75 3rd Qu.:3.75 3rd Qu.:3.0 3rd Qu.:3.75 3rd Qu.:4.75 3rd Qu.:4.0
Max. :5.00 Max. :4.00 Max. :5.0 Max. :5.00 Max. :5.00 Max. :5.0
View(subject)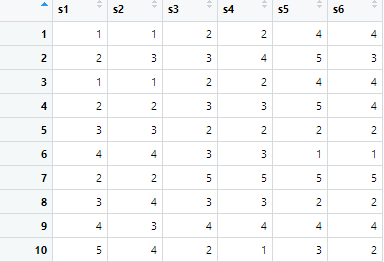
-- R은 4.0, 3.0, 4.0, 4.0, 2.0 으로 저장, 자료형 = numeric
- 변수의 주요 성분분석
pc <- prcomp(subject)
summary(pc)
-출력값-
PC1 PC2 PC3 PC4 PC5 PC6
표준편차 : Standard deviation 2.389 1.5532 0.87727 0.56907 0.19315 0.12434
분산비율 : Proportion of Variance 0.616 0.2603 0.08305 0.03495 0.00403 0.00167
누적비율 : Cumulative Proportion 0.616 0.8763 0.95936 0.99431 0.99833 1.00000
plot(pc)누적 비율(Cumulative Proportion) :
pc1 = 1개 그룹(분산 비율 : pc1) = 62% - 손실 38%
pc2 = 2개 그룹(분산 비율 : pc1 + pc2) = 88% - 12%
pc3 = 3개 그룹(분산 비율 : pc1 + pc2 + pc3) = 96% - 손실 4%
pc4 = 4개 그룹(분산 비율 : pc1 + pc2 + pc3 + pc4) = 99.4% - 손실 0.6%
pc5 = 5개 그룹(분산 비율 : pc1 + pc2 + pc3 + pc4 + pc5) = 99.8% - 손실 0.2%
pc6 = 6개 그룹(분산 비율 : pc1 + pc2 + pc3 + pc4 + pc5 + pc6) = 100% - 손실 0%
3개의 구룹으로 묶음 - (자연과학+물리화학) + (인문사회+신문방송) + 응용수학+추론통계) = 96%
해석 : 3개의 그룹으로 묶으면 96% 의미를 가져갈 수 있다(절대성의 의미X - 무조건 3그룹으로 묶을 필요X)
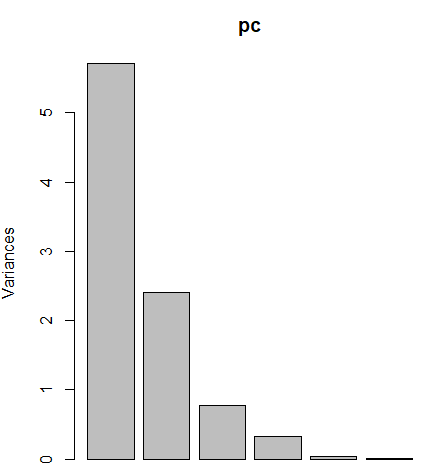
- 분산비율 : Proportion of Variance 시각화
- 고유값으로 요인 수 분석
en <- eigen(cor(subject))
# $values : 고유값, $vectors : 고유벡터 , cor : 상관 변수간에 상관 계수를 계산 - 상관분석
names(en) 출력값 : "values" "vectors"
en$values # $values : 고유값(스칼라) 보기 - 선택의 근거를 만듦
출력값 : [1] 3.44393944 1.88761725 0.43123968 0.19932073 0.02624961 0.01163331
plot(en$values, typ="o") # 고유값을 이용한 시각화 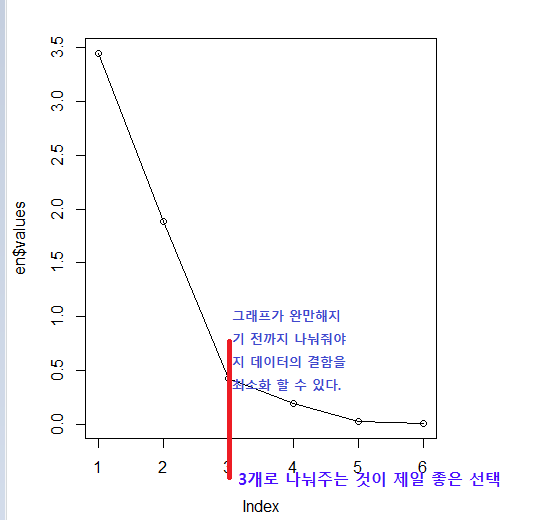
결론 : index 3까지 급현한 변화를 가지는데, 3개의 요인으로 remodeling 하면 최소의 오차를 가져가면서 성분에 대한 것을 가져갈 수 있을 것이다.
- 무조건 이렇게 설정할 필요 x , 판단은 사람에 따라 다를 수 있습니다.
- 변수 간의 상관관계 분석과 요인분석
cor(subject) # 상관계수의 값을 피드백 cor : 상관 변수간에 상관 계수를 계산
- 연관성에 대한 수치화 ( 값이 1에 가까울수록 연관성이 크다 )
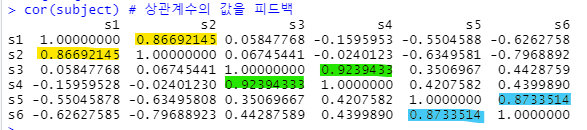
상관도(유사성)가 높은 그룹 : s1 - s2 = 86.6% , s3 - s4 = 92.3% , s5 - s6 = 87.3%
결론 : 3개의 그룹으로 합치는 것이 좋을 것이다.
요인분석 : 요인회전법 적용(varimax is the default)
① 주성분분석의 가정에 의해서 2개 요인으로 분석
result <- factanal(subject, factors = 2, rotation = "varimax")
result # p-value is 0.0232 < 0.05 # 요인수가 부족.
유의 확률 값 = 0.0232 < 0.05 = 기각
결과 : 2개로 결합하는 것은 적합하지 않다. 많은 성분들이 손실한다.
② 고유값으로 가정한 3개 요인으로 분석
result <- factanal(subject, factors = 3, # 요인 개수 지정
rotation = "varimax", # 회전방법 지정("varimax", "promax", "none")
scores="regression") # 요인점수 계산 방법
result
적절할 때는 유의 확률 값을 축출하지 않습니다. = 적절함
해설:

요인 적재량 보기
names(result)
result$loadings
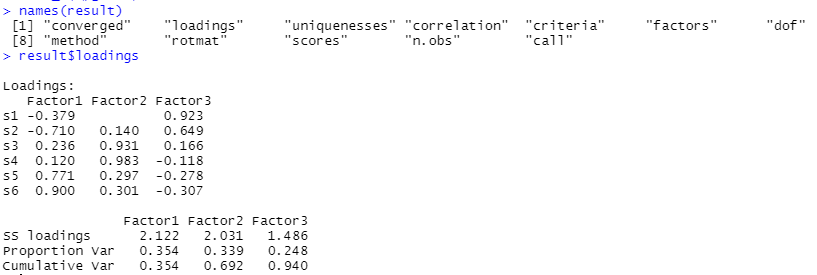
③ 다양한 방법으로 요인적재량 보기
print(result, digits = 2, cutoff=0.5)
print(result$loadings, cutoff=0) # display every loadings- print(result, digits = 2, cutoff=0.5)
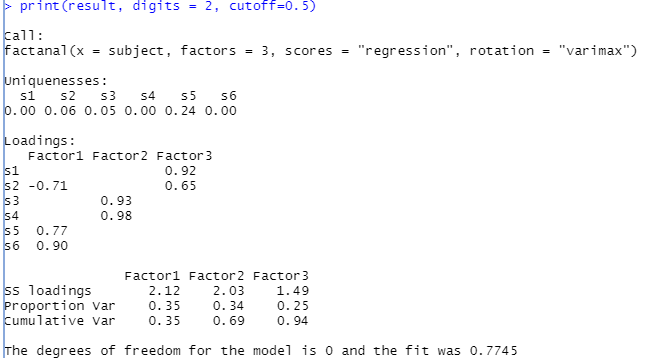
- print(result$loadings, cutoff=0) # display every loadings

요인점수
- 관측치의 동작을 살펴보는데 사용되며, 상관분석이나 회귀분석의 독립변수로 사용
- 각 변수(표준화값)와 요인 간의 관계(요인부하량)를 통해서 구해진 점수
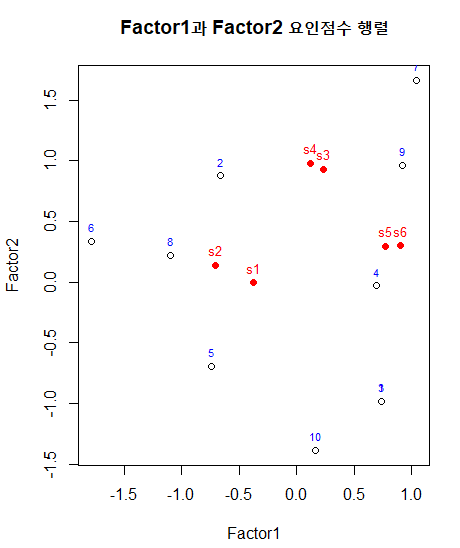
요인점수를 이용한 요인적재량 시각화
- Factor1, Factor2 요인지표 시각화
plot(result$scores[, c(1:2)], main="Factor1과 Factor2 요인점수 행렬")
text(result$scores[, 1], result$scores[,2],
labels = name, cex = 0.7, pos = 3, col = "blue")
- Factor1, Factor2 요인지표 시각화 + 요인적재량 plotting
points(result$loadings[, c(1:2)], pch=19, col = "red")
text(result$loadings[, 1], result$loadings[,2],
labels = rownames(result$loadings),
cex = 0.8, pos = 3, col = "red")
- Factor1, Factor3 요인지표 시각화
plot(result$scores[,c(1,3)], main="Factor1과 Factor3 요인점수 행렬")
text(result$scores[,1], result$scores[,3],
labels = name, cex = 0.7, pos = 3, col = "blue")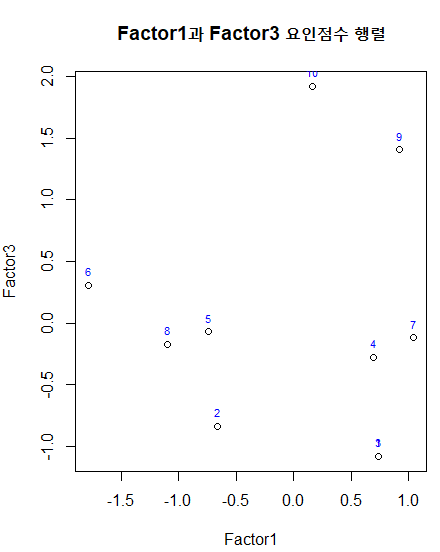
- Factor1, Factor3 요인지표 시각화 + 요인적재량 plotting
points(result$loadings[,c(1,3)], pch=19, col = "red")
text(result$loadings[,1], result$loadings[,3],
labels = rownames(result$loadings),
cex = 0.8, pos = 3, col = "red")
3차원 산점도로 요인적재량 시각화
install.packages("scatterplot3d")
library(scatterplot3d)
Factor1 <- result$scores[,1]
Factor2 <- result$scores[,2]
Factor3 <- result$scores[,3]
# scatterplot3d(밑변, 오른쪽변, 왼쪽변, type='p') # type='p' : 기본산점도 표시
d3 <- scatterplot3d(Factor1, Factor2, Factor3)
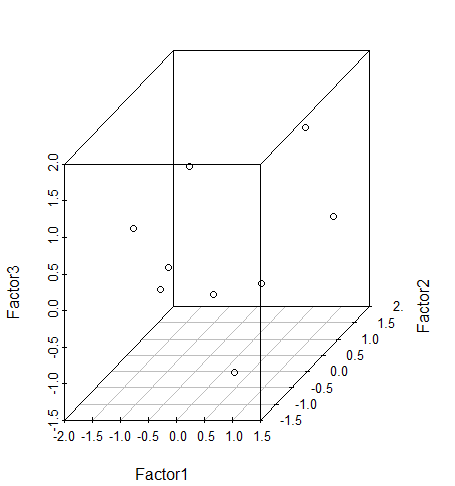
- 요인적재량 표시
loadings1 <- result$loadings[,1]
loadings2 <- result$loadings[,2]
loadings3 <- result$loadings[,3]
d3$points3d(loadings1, loadings2, loadings3, bg='red',pch=21, cex=2, type='h')
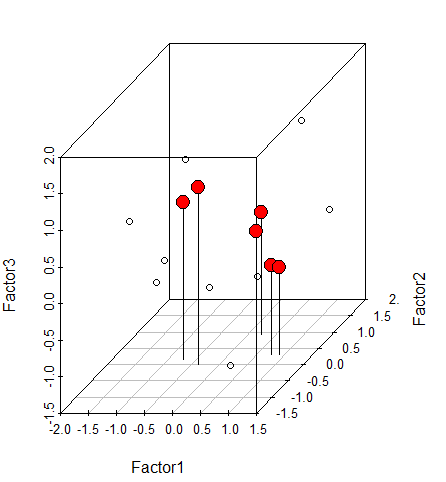
요인별 변수 묶기
① 요인별 과목변수 이용 데이터프레임 생성
app <- data.frame(subject$s5, subject$s6) # 응용과학
soc <- data.frame(subject$s3, subject$s4) # 사회과학
net <- data.frame(subject$s1, subject$s2) # 자연과학
② 산술평균 계산 - 3개의 파생변수 생성 : 가독성과 설득력이 높다.
app_science <- round( (app$subject.s5 + app$subject.s6) / ncol(app), 2)
soc_science <- round( (soc$subject.s3 + soc$subject.s4) / ncol(soc), 2)
net_science <- round( (net$subject.s1 + net$subject.s2) / ncol(net), 2)
③ 상관관계 분석 - 요인분석을 통해서 만들어진 파생변수는 상관분석이나 회귀분석에서 독립변수로 사용할 수 있다.
subject_factor_df <- data.frame(app_science, soc_science, net_science)
cor(subject_factor_df)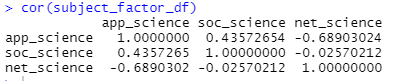
2. 잘못 분류된 요인 제거로 변수 정제
- 요인분석에 사용될 데이터 셋 가져오기
① 데이터 가져오기
install.packages('memisc') # spss tool 포맷 파일 읽어오기
library(memisc)
setwd("C:/workspaces/R/data/")
data.spss <- as.data.set(spss.system.file('drinking_water.sav', , encoded = 'utf-8'))
head(data.spss)
- 출력값 -
Data set with 20 observations and 15 variables
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11 성별 연령 지역 학력
1 3 2 3 3 4 3 4 3 4 3 4 32@Z 204k 4k18 @|9.4kA9
2 3 3 3 3 3 3 2 3 3 2 3 2 204k 4k18 @|9.4kA9
3 3 3 3 4 3 4 3 4 4 4 4 32@Z 204k 4k18 0mA9
4 3 3 3 1 3 2 3 2 2 2 2 2 204k 4k18 @|9.4kA9
5 3 3 2 2 3 3 2 2 2 2 2 2 204k 4k18 @|9.4kA9
6 1 1 1 1 1 1 1 3 3 3 3 32@Z 304k 4k18 @|9.4kA9
7 2 2 2 3 2 3 5 4 4 4 4 2 204k 4k18 4kA9
8 2 2 1 2 1 2 1 2 2 2 2 2 204k 4k18 @|9.4kA9
9 2 2 1 2 3 3 1 3 2 3 1 2 204k 4k18 4kA9
10 4 3 3 3 4 3 3 4 2 3 4 2 204k 4k18 5
11 3 4 4 3 4 4 4 5 5 5 5 2 204k 4k18 4kA9
12 2 1 1 2 2 2 1 4 4 5 5 32@Z 204k 4k18 0mA9
13 1 1 1 2 1 1 1 1 1 1 1 2 204k 4k18 @|9.4kA9
14 2 3 2 2 3 1 2 3 2 2 2 2 204k 4k18 @|9.4kA9
15 1 2 2 1 1 1 1 2 2 2 2 32@Z 304k 4k18 @|9.4kA9
16 3 2 2 2 3 2 2 2 2 2 1 32@Z 204k 4k18 @|9.4kA9
17 3 3 3 3 2 3 2 3 3 3 3 2 204k 4k18 @|9.4kA9
18 3 3 3 3 2 2 2 2 3 3 2 2 204k 4k18 @|9.4kA9
19 3 3 2 2 3 2 2 3 3 3 3 2 204k 4k18 @|9.4kA9
20 4 4 4 4 4 4 3 4 4 4 4 2 204k 4k18 @|9.4kA9
View(data.spss)
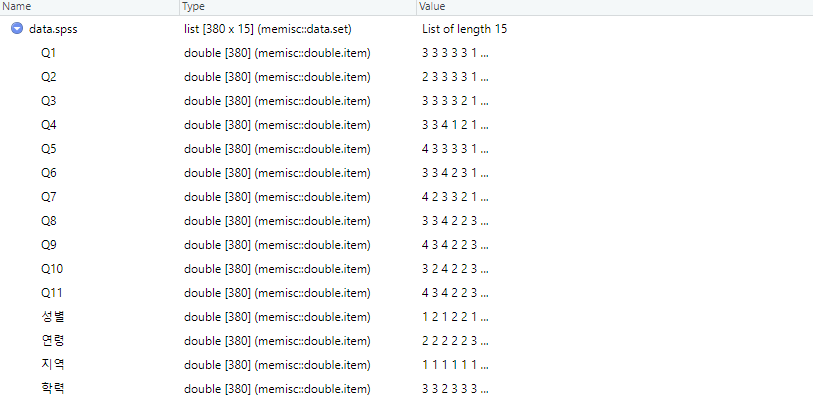

② 데이터프레임으로 변경
drinking_water <- data.spss[1:11]
drinking_water
- 출력값 -
Q1 Q2 Q3 Q4 Q5 Q6 Q7 Q8 Q9 Q10 Q11
1 3 2 3 3 4 3 4 3 4 3 4
2 3 3 3 3 3 3 2 3 3 2 3
3 3 3 3 4 3 4 3 4 4 4 4
4 3 3 3 1 3 2 3 2 2 2 2
5 3 3 2 2 3 3 2 2 2 2 2
6 1 1 1 1 1 1 1 3 3 3 3
7 2 2 2 3 2 3 5 4 4 4 4
8 2 2 1 2 1 2 1 2 2 2 2
9 2 2 1 2 3 3 1 3 2 3 1
10 4 3 3 3 4 3 3 4 2 3 4
11 3 4 4 3 4 4 4 5 5 5 5
12 2 1 1 2 2 2 1 4 4 5 5
13 1 1 1 2 1 1 1 1 1 1 1
14 2 3 2 2 3 1 2 3 2 2 2
15 1 2 2 1 1 1 1 2 2 2 2
16 3 2 2 2 3 2 2 2 2 2 1
17 3 3 3 3 2 3 2 3 3 3 3
18 3 3 3 3 2 2 2 2 3 3 2
19 3 3 2 2 3 2 2 3 3 3 3
20 4 4 4 4 4 4 3 4 4 4 4
21 3 4 2 1 1 1 1 3 2 3 1
22 4 2 2 1 1 1 1 3 4 4 1
23 3 3 2 2 2 2 3 2 3 3 3
24 2 2 2 2 2 3 1 4 4 4 2
25 2 2 2 2 2 2 3 4 3 3 3
.. .. .. .. .. .. .. .. .. .. ... ...
(25 of 380 observations shown)
drinking_water_df <- as.data.frame(drinking_water)
str(drinking_water_df)
- 출력값 -
'data.frame': 380 obs. of 11 variables:
$ Q1 : num 3 3 3 3 3 1 2 2 2 4 ...
$ Q2 : num 2 3 3 3 3 1 2 2 2 3 ...
$ Q3 : num 3 3 3 3 2 1 2 1 1 3 ...
$ Q4 : num 3 3 4 1 2 1 3 2 2 3 ...
$ Q5 : num 4 3 3 3 3 1 2 1 3 4 ...
$ Q6 : num 3 3 4 2 3 1 3 2 3 3 ...
$ Q7 : num 4 2 3 3 2 1 5 1 1 3 ...
$ Q8 : num 3 3 4 2 2 3 4 2 3 4 ...
$ Q9 : num 4 3 4 2 2 3 4 2 2 2 ...
$ Q10: num 3 2 4 2 2 3 4 2 3 3 ...
$ Q11: num 4 3 4 2 2 3 4 2 1 4 ...
③ 요인수를 3개로 지정하여 요인분석 수행
result2 <- factanal(drinking_water_df, factors = 3, rotation = "varimax",
scores = "regression")
print(result2, cutoff=0.5)result2

- print(result2, cutoff=0.5)

Q4의 값이 파악한 바와 알고리즘으로 도출된 것이 다를 때, 이러한 요인의 변수값은 제거해서 처리해서 하는 것이 정확한 값을 피드백 받을 수 있습니다.
요인별 변수 묶기
① q4 칼럼 제외하여 데이터프레임 생성
dw_df <- drinking_water_df[-4] - 4번째열 제외 (Q4)
str(dw_df)
- 출력값 -
'data.frame': 380 obs. of 10 variables:
$ Q1 : num 3 3 3 3 3 1 2 2 2 4 ...
$ Q2 : num 2 3 3 3 3 1 2 2 2 3 ...
$ Q3 : num 3 3 3 3 2 1 2 1 1 3 ...
$ Q5 : num 4 3 3 3 3 1 2 1 3 4 ...
$ Q6 : num 3 3 4 2 3 1 3 2 3 3 ...
$ Q7 : num 4 2 3 3 2 1 5 1 1 3 ...
$ Q8 : num 3 3 4 2 2 3 4 2 3 4 ...
$ Q9 : num 4 3 4 2 2 3 4 2 2 2 ...
$ Q10: num 3 2 4 2 2 3 4 2 3 3 ...
$ Q11: num 4 3 4 2 2 3 4 2 1 4 ...
dim(dw_df) 출력값 : [1] 380 10
cor(dw_df)
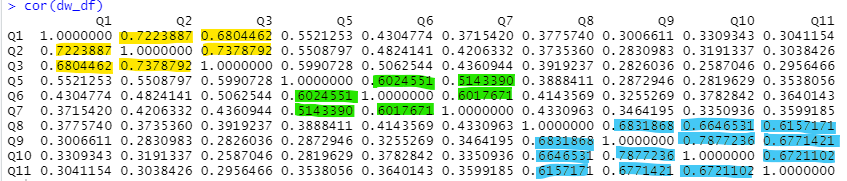
Q1~3(제품 친밀도) , Q5~7(제품적절성) , Q8~11(제품만족도)
② 요인에 속하는 입력변수별 데이터프레임 구성
제품만족도 저장 데이터프레임
s <- data.frame(dw_df$Q8, dw_df$Q9, dw_df$Q10, dw_df$Q11)
제품친밀도 저장 데이터프레임
c <- data.frame(dw_df$Q1, dw_df$Q2, dw_df$Q3)
제품적절성 저장 데이터프레임
p <- data.frame(dw_df$Q5, dw_df$Q6, dw_df$Q7)
③ 요인별 산술평균 계산
satisfaction <- round( (s$dw_df.Q8 + s$dw_df.Q9 + s$dw_df.Q10 + s$dw_df.Q11) / ncol(s), 2)
closeness <- round( (c$dw_df.Q1 + c$dw_df.Q2 + c$dw_df.Q3) / ncol(c), 2)
pertinence <- round( (p$dw_df.Q5 + p$dw_df.Q6 + p$dw_df.Q7) / ncol(p), 2)
④ 상관관계 분석
drinking_water_factor_df <- data.frame(satisfaction, closeness, pertinence)
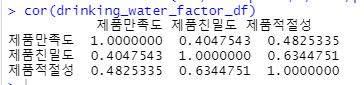
colnames(drinking_water_factor_df) <- c("제품만족도","제품친밀도","제품적절성")
cor(drinking_water_factor_df)
'빅데이터 > R' 카테고리의 다른 글
| [R] 머신러닝(Machine Learning) (0) | 2020.07.17 |
|---|---|
| [R] 상관관계 분석(Correlation Analysis) (0) | 2020.07.17 |
| [R] 집단 간 차이 분석 (part_3 세 집단 분석(분산 분석)) (0) | 2020.07.16 |
| [R] 집단 간 차이 분석 (part_2 두 집단 분석) (0) | 2020.07.15 |
| [R] 집단 간 차이 분석 (part_1 단일 집단 분석) (0) | 2020.07.15 |




