Practice makes perfect
[DeepLearning] 넘파이(NumPy) 본문
넘파이 (NumPy , Numerical Python)
: 파이썬에서 선형대수 기반의 프로그램을 쉽게 만들 수 있도록 지원하는 대표적 인 패키지로 대량 데이터의 배열 연산을 가능하게 하므로 빠른 배열 연산 속도를 보장합니다.
넘파이 특징
- C/C++ 과 같은 저수준 언어 기반의 호환 API 를 제공합니다.
- 파이썬 언어 자체가 가지는 수행 성능의 제약이 있으므로 수행 성능이 매우 중요한 부분은 C/C++ 기반의 코드로
작성하고 이를 넘파이에서 호출하는 방식으로 쉽게 통합 가능합니다.
- 다양한 데이터 핸들링 기능도 제공합니다.
- 넘파이 array() 함수는 파이썬의 리스트와 같은 다양한 인자를 입력 받아서 ndarray 로 변환하는 기능을 수행합니다.
넘파이 모듈의 임포트 방법
- import numpy as np
- 넘파이 기반 데이터 타 입 : ndarray
1. 배열 생성
① 1차원 배열(Vector) 정의
arr = np.array([1,2,3])
print(arr) # [1 2 3]
print(type(arr)) # <class 'numpy.ndarray'>
출력값
[1 2 3]
② 2차원 배열(Matrix) 정의
arr2 = np.array([[1,2,3],[4,5,6]]) # 2행 3열
print(arr2)
출력값
[[1 2 3]
[4 5 6]]
print(type(arr2)) 출력값 : <class 'numpy.ndarray'>
print("arr2.shape:{0}".format(arr2.shape)) 출력값 : (2, 3)
③ 3차원 배열(Array) 정의
# 2면 2행 3열
arr3 = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
print(arr3)
출력값
[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
print("arr3.shape:{0}".format(arr3.shape)) 출력값: (2, 2, 3) 2면 2행 3열
2. 배열 생성 및 초기화
① zeros((행, 열)): 0으로 채우는 함수
arr_zeros = np.zeros((3,4)) 3행 4열
print(arr_zeros)
출력값
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
② ones((행, 열)): 1로 채우는 함수
arr_ones = np.ones((2,2)) # 2행 2열
print(arr_ones)
출력값
[[1. 1.]
[1. 1.]]
③ full((행, 열), 값): 값으로 채우는 함수
arr_full = np.full((3, 4), 7) # 3행 4열
print(arr_full)
- 출력값 -
[[7 7 7 7]
[7 7 7 7]
[7 7 7 7]]
④ eye(N): (N,N)의 단위 행렬 생성
arr_eye = np.eye(5)
print(arr_eye)
- 출력값 -
[[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]]
⑤ empty((행, 열)): 초기화 없이 기존 메모리 값이 들어감
arr_empty = np.empty((3,3))
print(arr_empty)
- 출력값 -
[[0.00000000e+000 0.00000000e+000 0.00000000e+000]
[0.00000000e+000 0.00000000e+000 5.92878775e-322]
[4.45042952e-307 2.55896735e-307 9.79101081e-307]]
⑥ _like(배열) 지정한 배열과 동일한 shape의 행렬을 만듦
arr_sample = np.array([[1,2,3],[4,5,6]])
arr_like = np.ones_like(arr_sample)
print(arr_like)
- 출력값 -
[[1 1 1]
[1 1 1]]- 종류: np.zeros_like(), np.ones_like(), np.full_like(), np.empty_like()
⑦ 배열 데이터 생성 함수
- np.linspace(시작, 종료, 개수): 개수에 맞게끔 시작과 종료 사이에 균등하게 분배
arr_linspace = np.linspace(1,10,5)
print(arr_linspace) 출력값 : [ 1. 3.25 5.5 7.75 10. ]
plt.plot(arr_linspace, 'o') # 그래프를 그려주는 함수 마커를 원('o')으로
plt.show() # 만든 그래프를 보여줌.

- np.arange(시작, 종료, 스텝): 시작과 종료 사이에 스텝 간격으로 생성
arr_arange = np.arange(1,20,2)
print(arr_arange)
출력값 : [ 1 3 5 7 9 11 13 15 17 19]
3. list vs ndarray(1차원 배열(Vector))
# list
x1 = [1,2,3]
y1 = [4,5,6]
print(x1+y1) 출력값 : [1, 2, 3, 4, 5, 6]
# ndarray(1차원 배열)
x2 = np.array([1,2,3])
y2 = np.array([4,5,6])
print(x2+y2) 출력값 : [5 7 9]
print(type(x1)) 출력값 : <class 'list'>
print(type(x2)) 출력값 : <class 'numpy.ndarray'>
print(x2[2]) 출력값 : 요소의 참조: 3
x2[2] = 10 - 요소의 수정
print(x2) 출력값 : [ 1 2 10]
- 연속된 정수 벡터의 생성
print(np.arange(10)) 출력값 : [0 1 2 3 4 5 6 7 8 9]
print(np.arange(5,10)) 출력값 : [5 6 7 8 9]
x = np.array([10,11,12])
for i in np.arange(1,4): # 1~3
print(i) # 1~3
print(i+x) # 1 + (([10,11,12])) , 2 + ([10,11,12]) , 3 + ([10,11,12])
- 출력값 -
1
[11 12 13]
2
[12 13 14]
3
[13 14 15]
- ndarray형의 주의점
a = np.array([1,1])
b = a # 주소값 복사
print('a = '+ str(a)) 출력값 : [1 1]
print('b = '+ str(b)) 출력값 : [1 1]
b[0] = 100
print('a = '+ str(a)) 출력값 : [100 1]
print('b = '+ str(b)) 출력값 : [100 1]
-------------------------------------------------------------------------------------
a = np.array([1,1])
b = a.copy()
print('a = '+ str(a)) 출력값 : [1 1]
print('b = '+ str(b)) 출력값 : [1 1]
b[0] = 100
print('a = '+ str(a)) 출력값 : [1 1]
print('b = '+ str(b)) 출력값 : [100 1]
- 행렬(2차원)
x = np.array([[1,2,3],[4,5,6]]) # 2행 3열
print(x)
- 출력값 -
[[1 2 3]
[4 5 6]]
print(type(x)) 출력값 : <class 'numpy.ndarray'>
print(x.shape) 출력값 : (2, 3) - 튜플
w, h = x.shape
print(w) 출력값 : 2
print(h) 출력값 : 3
print(x[1,2]) 출력값 : 6
x[1,2] = 10 # 요소의 수정
print(x)
- 출력값 -
[[ 1 2 3]
[ 4 5 10]]
- 행렬의 크기 변경
a = np.arange(10)
print(a)
출력값 : [0 1 2 3 4 5 6 7 8 9]
a_arange = a.reshape(2,5) # 행렬의 크기를 변형 : reshape
print(a_arange)
- 출력값 -
[[0 1 2 3 4]
[5 6 7 8 9]]
print(type(a_arange)) 출력값 : <class 'numpy.ndarray'>
print(a_arange.shape) 출력값 : (2, 5)
- 스칼라 x 행렬
스칼라 : 값이 한개인 변수
x = np.array([[4,4,4],[8,8,8]])
scar_arr = 10 * x
print(scar_arr)
- 출력값 -
[[40 40 40]
[80 80 80]]
산술함술 : np.exp(x) - 지수 함수 , np.sqrt() - 루트 씌운 값, np.log() - 로그 함수 , np.round() - 반올림,
np.mean() - 평균, np.std() - 표준편차, np.max() - 최대 , mp.min() - 최소
x = np.array([[4,4,4],[8,8,8]])
print(np.exp(x)) # 지수 함수 : y = e(x제곱)
- 출력값 -
[[ 54.59815003 54.59815003 54.59815003]
[2980.95798704 2980.95798704 2980.95798704]]
- 내적의 곱
x = np.array([[1,2,3],[4,5,6]])
y = np.array([[7],[7],[7]])
print(x.dot(y))
- 출력값 -
(2x1)
[[ 42] - > (1*7)+(2*7)+(3*7)
[105]] - > (4*7)+(5*7)+(6*7)
x = np.array([[1,2,3],[4,5,6]])
y = np.array([[7,2],[7,2],[7,2]])
print(x.dot(y))
- 출력값 -
(2x2)
[[ 42 12] - > (1*7)+(2*7)+(3*7) (1*2)+(2*2)+(3*2)
[105 30]] - > (4*7)+(5*7)+(6*7) (4*2)+(5*2)+(6*2)
- 원소 접근
data = np.array([[51,55],[14,19],[0,4]])
print(data)
print(data.shape) # (3, 2)
print(data[0][1]) # 55 행렬의 인덱스로 접근
for row in data:
print(row)
- 출력값 -
[51 55]
[14 19]
[0 4]
y = data.flatten() --> data를 1차원 배열로 변환(평탄화)
print(y) 출력값 : [51 55 14 19 0 4] // ( 3 , 2 ) -> 1차원 배열
- 슬라이싱
x = np.arange(10)
print(x[:5]) 출력값 : [0 1 2 3 4]
print(x[5:]) 출력값 : [5 6 7 8 9]
print(x[3:8]) 출력값 : [3 4 5 6 7]
print(x[3:8:2]) 출력값 : [3 5 7]
print(x[::-1]) 출력값 : [9 8 7 6 5 4 3 2 1 0]
y = np.array([[1,2,3],[4,5,6],[7,8,9]]) # 3행 3열
print(y[:2,1:2]) 출력값 : (0,1),(1,1)
- 출력값 -
[[2]
[5]]
- 조건을 만족하는 데이터 수정
- bool 배열 사용
x = np.array([1,1,2,3,4,5,8,15]) # list -> array
print(x > 3) # array 와 비교 연산사를 사용하면 boolean 값이 출력
출력값 : [False False False False True True True True]
y = x[x > 3] # true인 데이터만 선택된다.
print(y) 출력값 : [ 4 5 8 15]
x[x > 3] = 555 # 조건이 일치하면 555 담겨진다.
print(x) 출력값 : [ 1 1 2 3 555 555 555 555]
# - Numpy에서 np.sum 한수의 axis 이해
arr = np.arange(0,4*2*4) # start = 0, end = 31
print(len(arr)) # 32(0~31)
v = arr.reshape([4,2,4]) # 차원의 변경(depth(z축), row(x축), colum(y축)) - (4면, 2행, 4열)
print(v)
- 출력값 -
[[[ 0 1 2 3]
[ 4 5 6 7]]
[[ 8 9 10 11]
[12 13 14 15]]
[[16 17 18 19]
[20 21 22 23]]
[[24 25 26 27]
[28 29 30 31]]]
print(v.shape) 출력값 : (4, 2, 4) : 4 면 2행 4열
print(v.ndim) 출력값 : v의 차원 : 3차원
print(v.sum()) 출력값 : 496 : 모든 요소의 합 : (0 ~ 31) 까지 더한 값
- axis
print(v.sum(axis=0)) # axis=0 : row 축(단위)로 계산 / 면단 위로
- 출력값 -
[[48 52 56 60] -> (0+8+16+24) (1+9+17+25) (2+10+18+26) (3+11+19+27)
[64 68 72 76]] -> (4+12+20+28) (5+13+21+29) (6+14+22+30) (7+15+23+31)
print(v.sum(axis=1)) # axis=1 : colum 축(단위)로 계산 / 행 당위
- 출력값 -
[[ 4 6 8 10] -> (0+4) (1+5) (2+6) (3+7)
[20 22 24 26] -> (8+12) (9+13) (10+14) (11+15)
[36 38 40 42] -> (16+20) (17+21) (18+22) (19+23)
[52 54 56 58]] -> (24+28) (25+29) (26+30) (27+31)
print(v.sum(axis=2)) # axis=2 : depth 축(단위)로 계산 / 열 단위
- 출력값 -
[[ 6 22] -> (0+1+2+3) (4+5+6+7)
[ 38 54] -> (8+9+10+11) (12+13+14+15)
[ 70 86] -> (16+17+18+19) (20+21+22+23)
[102 118]] -> (24+25+26+27) (28+29+30+31)
4. 그래프 그리기
- 데이터 준비
x = np.arange(0,6,0.1) # start 0 ~ last 5 , step = 0.1 (0.1~5.9)
y1 = np.sin(x) # 사인함수 를 이용하여 0.1단위로 계산해서 y1에 저장
y2 = np.cos(x) # 코사인함수 를 이용하여 0.1단위로 계산해서 y2에 저장
- 그래프 그리기
plt.plot(x, y1, label = "sin")
plt.plot(x, y2, linestyle = "--", label = "cos") # cos 함수는 점선으로 그리기
plt.xlabel("x") # x축 이름
plt.ylabel("y") # y축 이름
plt.title("sin & cos") # 제목
plt.legend() # 범례
plt.show() # 출력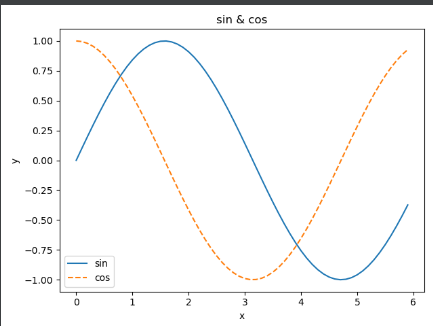
- 꺽은선 그래프
x = np.arange(10)
y = np.random.rand(10)
plt.plot(x,y) # 꺽은선 그래프를 등록 / 10개의 난수를 plot 함수를 이용하여 꺽은석 그래프로 피드백.
plt.show() # 그래프 그리기
- 3차 함수 f(x) = (x-2) x (x+2)
def f(x):
return (x-2) * x * (x+2) # 3차 함수 정의
print(f(0)) 출력값 : 0
print(f(2)) 출력값 : 0
print(f(-2)) 출력값 : 0
# x값에 대해 ndarray 배열이며 각각에 대한 f를 한꺼번에 ndarray로 돌려줍니다.
print(f(np.array([1,2,3]))) 출력값 : [-3 0 15]
print(type(f(np.array([1,2,3])))) 출력값 : <class 'numpy.ndarray'>
# 그래프를 그리는 x의 범위를 -3 ~ 3까지로 하고 , 간격 0.5
x = np.arange(-3,3.5,0.5)
plt.plot(x,f(x))
plt.show()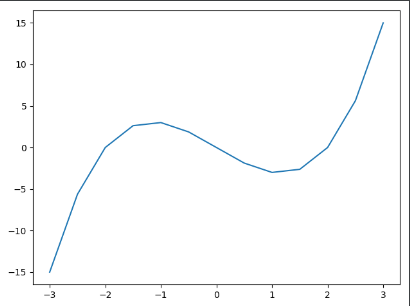
- 그래프를 장식
x = np.linspace(-3,3,100) # x를 100 분할하기
# 차트 묘사
plt.plot(x, f2(x,2), color = "black")
plt.plot(x, f2(x,1), color = "blue")
plt.legend(loc="upper left") # 범례의 위치도 정해줄 수 있다.
plt.ylim(-15,15) # y축 범위
plt.title("f2(x, w) 함수")
plt.xlabel("x축")
plt.ylabel("y축")
plt.grid(True) # 그리드(눈금)
plt.show()
- 그래프를 여러 개 보여주기
plt.figure(figsize=(10,3)) # 전체 영역의 크기를 지정
plt.subplots_adjust(wspace=0.5, hspace=0.5) # 그래프의 간격을 지정
for i in range(6): # 0 ~ 5
plt.subplot(2, 3, i+1) # 그래프 위치를 지정 # 2행 3열
plt.title(i+1)
plt.plot(x,f2(x,i))
plt.ylim(-20,20)
plt.grid(True)
plt.show()
- 이미지 표시하기
from matplotlib.image import imread
img = imread('image/2.png') # 이미지 읽어오기
plt.imshow(img)
plt.show()
'Anaconda > DeepLearning' 카테고리의 다른 글
| [DeepLearning] 오차역전파법 (backpropagation) (0) | 2020.08.10 |
|---|---|
| [DeepLearning] 확률적 경사 하강법(SGD), 학습 알고리즘 구현 (0) | 2020.08.07 |
| [DeepLearning] 신경망 학습 (0) | 2020.08.06 |
| [DeepLearning] 신경망(neural network) (0) | 2020.08.04 |
| [DeepLearning] 퍼셉트론(perceptron) (0) | 2020.08.03 |




