Practice makes perfect
[DeepLearning] 신경망 학습 본문
신경망
: 퍼셉트론에서 출발하여 여러 입력신호를 입력받아서 출력을 내보내주는 표현이 퍼셉트론이었는데, 퍼셉트론과의 차이는 활성화 함수를 어떤 것을 사용하느냐에 차이를 가집니다. 퍼셉트론은 스텝 함수를 사용하고, 신경망은 시그모이드 함수를 사용합니다. 스텝 함수는 선형성이고, 시그모이드 비선형입니다. 게이트를 통해서 결과를 확인할 때, XOR는 비선형의 형태를 통해서 코드상으로 구현할 수 있습니다. 코드의 형태를 봤을 때, 입력과 출력의 형태로만 되어있던 것을 은닉층을 통해 다층의 구조를 가져갈 때, 활성화 함수를 시그모이드 함수로 활용하여 선형적으로 절대 분류 할 수 없었던 특징을 비선형으로 구현할 수 있게 되었습니다.

신경망 학습 : 데이터로부터 매개변수의 값을 정하는 방법
- ex) y = ax + b / a(기울기) , b(절편) 을 획득하라.
신경망의 특징
- 데이터를 보고 학습할 수 있다.
- 가중치 매개변수의 값을 데이터를 보고 자동으로 결정한다는 뜻.
- 사람의 개입을 최소화하고, 수집한 데이터로부터 답을 찾고, 패턴을 찾으려는 시도
- 특히, 신경망과 딥러닝은 기존 기계학습에서 사용하던 방법보다 사람의 개입을 더욱 배제할 수 있게 해주는 중요한
특성을 지님
훈련 데이터와 시험 데이터
훈련 데이터 (training data)
: 훈련 데이터만 사용하여 학습하면서 최적의 매개변수를 찾음
시험 데이터 (test data)
: 앞서 훈련한 모델의 실력을 평가하는 것
훈련 / 시험 데이터 분리 이유
: 우리가 원하는 것은 범용적으로 사용할 수 있는 모델 구현
: 범용 능력을 제대로 평가하기 위해 모델을 찾아내는 것이 기계 학습의 최종 목표
오버피팅 (overfitting) : 한 데이터 셋에만 지나치게 최적화된 상태
- 학습용 데이터를 넣을 때는 정확하지만, 테스트 데이터를 넣었을 때는 결과가 정확하지 않은 것.
손실 함수(loss function)
: 손실함수는 신경망을 학습할 때 학습 상태에 대해 측정할 수 있도록 해주는 지표입니다. 신경망의 가중치 매개변수들이 스스로 특징을 찾아 가기에 이 가중치 값의 최적이 될 수 있도록 해야 하며 잘 찾아가고 있는지 볼 때 손실 함수를 보는 것입니다 = 손실 함수의 결과값을 가장 작게 만드는 가중치 매개 변수를 찾는 것이 학습의 목표.
- 데이터와 그래프와의 거리의 오차가 가장 작은 범위를 찾아서 머신러닝/딥러닝을 통해서 찾도록 하는 것입니다.


1) 평균 제곱 오차(mean squared error, MSE) - 회귀분석
: 평균제곱오차는 손실 함수로 가장 많이 쓰이며 간단하게 설명하면 예측하는 값이랑 실제 값의 차이(error)를 제곱하여 평균을 낸 것이 평균제곱오차입니다. 예측 값과 실제 값의 차이가 클수록 평균제곱오차의 값도 커진다는 것은 이 값이
작을 수록 예측력이 좋다고 할 수 있습니다.

pi = 실제값 , yi - 예측값
MSE(Mean Squared Error)
def mean_squared_error(y, t): # p와 y 자리가 바뀌어도 제곱을 할것이기 때문에 문제 없다.
return np.sum((y-t) ** 2) # 제곱
# 2 : 정답
t = [0,0,1,0,0,0,0,0,0,0] # 답 2 : 원핫인코딩(One-Hot Encording)
# 예측 결과 : 2
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
msq = mean_squared_error(np.array(t),np.array(y)) # 리스트 형태 -> 배열로 변환
print(msq)
출력값 : 0.19500000000000006
# 예측 결과 : 7
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
msq = mean_squared_error(np.array(t),np.array(y)) # 리스트 형태 -> 배열로 변환
print(msq)
출력값 : 1.195
- 제곱을 한다는 것은 면적을 구하는 것으로, 그 면적의 제곱이 더 작은 기울기를 찾는 것입니다. 왼쪽 보다 오른쪽이 더잘 찾은 그래프 입니다.
2) 교차 엔트로피 오차(cross entropy error, CEE) - 분류분석
: 교차 엔트로피 오차는 정답일 때의 출력이 전체 값을 정하게 됩니다. 데이터 하나에 대한 손실 함수에서 N개의 데이터로 확장. 다만, N으로 나누어 정규화. 평균 손실 함수, 교차엔트로피는 로그의 밑이 e인 자연로그를 예측값에 씌워서 실제 값과 곱한 후 전체 값을 합한 후 음수로 변환합니다. 실제 값이 원핫인코딩(one-hot encoding; 더미변수처럼 1~9까지 범주로 했을 때 정답이 2일 경우 2에는 '1'을 나머지 범주에는 '0'으로) 방식 일경우에는 2를 제외한 나머지는 무조건 0이 나오므로 실제값일 때의 예측값에 대한 자연로그를 계산하는 식이 됩니다. 실제 값이 2인데 0.6으로 예측했다면 교차 엔트로피 오차는 -log(1*0.6) = -log0.6 이 된다. = 0.51
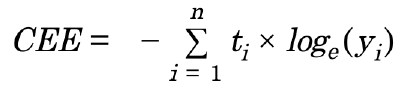
ti : 정답 레이블 , yi : 예측값
CEE(Cross Entropy Error)
def cross_entropy_error(t, y):
delta = 1e-7 # NaN 값이 나오지 않기 위함
return -np.sum(t * np.log(y+delta))
# 2 : 정답
t = [0,0,1,0,0,0,0,0,0,0] # 답 2 : 원핫인코딩(One-Hot Encording)
# 예측 결과 : 2
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
cee = cross_entropy_error(np.array(t),np.array(y)) # 리스트 형태 -> 배열로 변환
print(cee)
출력값 : 0.510825457099338
# 예측 결과 : 7
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cee = cross_entropy_error(np.array(t),np.array(y)) # 리스트 형태 -> 배열로 변환
print(cee)
출력값 : 2.302584092994546
자연로그y=log𝑥의 그래프
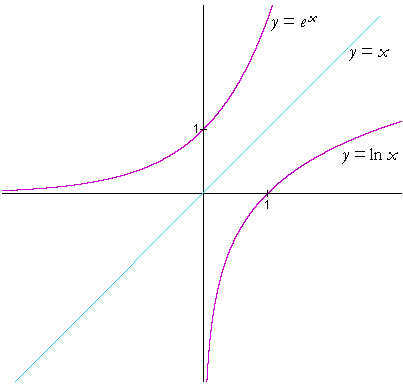
: 교차 엔트로피는 출력이 1일 때 0이 되며 x가 커질수록 0에 가까워지고 x가 작아질수록(0에 가까워질수록) 값이 작아집니다(음의방향).
미니배치 학습
: 한번에 하나만 계산하는게 아니라 일부를 조금씩 가져와서 전체의 '근사치'로 이용하여 일분만 계속 사용하여 학습을 수행하는 방법을 이용합니다. 그 일부를 미니배치 mini-batch 라고 합니다. 훈련 데이터에서 일부를 무작위로 뽑아 학습하는 것은 미니배치 학습입니다. 미니배치는 무작위로 추출하는 것으로 표본을 무작위로 샘플링하는 것과 개념적으로 유사합니다.
import numpy as np
from dataset.mnist import load_mnist
# 60000개 데이터 10000개 데이터
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# normalize= True : 정규화 , one_hot_label= True : 원핫인코딩 방식으로 처리
print(x_train.shape) # (60000, 784) 60000개 데이터, 784 입력 개수
print(t_train.shape) # (60000, 10) one_hot_label=True - 1이 아닌 10으로 불러온다.
print(t_train.shape[0]) # 60000 : 전체 데이터의 개수를 출력한다.
print(t_train.shape[1]) # 10 : one_hot_label=True 에 의해서 10으로 출력.
batch_size = 100 # 60000개 중에서 batch 100
# 지정한 범위의 수 중에서 무작위로 원하는 개수만 선택(batch_size = 100).
batch_mask = np.random.choice(t_train.shape[0], batch_size)
# (범위,출력개수) - 60000개 중에서 100개 index를 출력
print(batch_mask)
출력값:
[10995 25334 55558 55950 43378 42591 59185 42772 37410 15106 19732 25420
36632 2856 19635 32958 44348 1958 2423 29217 32011 32203 6246 3725
36512 9584 5884 39660 55198 54392 10831 17019 29137 33830 34056 48376
40238 45480 37854 1991 26662 4218 24518 2198 3433 58183 49781 32639
49820 58634 22093 3984 58591 54007 44081 49513 34769 27648 2329 24193
7408 56742 55155 14269 59064 45151 54338 42582 7501 36434 15837 49116
26964 21467 29748 3811 55781 1606 16729 15604 3548 5645 8241 5217
26850 29007 50469 26448 41770 59517 28124 45990 40545 12044 27309 29817
35131 34838 14644 35117]
미분 - 접선의 기울기를 구하는 개념
: 경사법에서는 기울기 값을 기준으로 방향을 정합니다.
- 미분은 한 순간의 변화량을 계산한 것(x 의 작은 변화 가 함수 f(x) 를 얼마나 변화시키느냐를 의미)
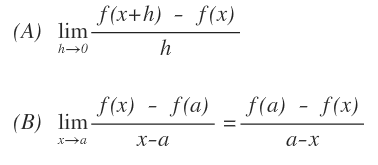
수치 미분
h는 시간을 뜻하고 이를 한 없이 0에 가깝게 한다는 의미로 lim를 주고, 분자는 a에 대한 변화량을 나타냅니다.
이와 같은 방식으로 미분을 구하는 것은 수치 미분이라고 합니다. 차분(임의의 두 점에서 함수 값들의 차이)으로 미분을 구하기 때문입니다. 수치 미분은 오차가 포함될 수 밖에 없습니다. 오차를 줄이기 위해서는 x를 중심으로 h 만큼의 함수 f의 차분을 계산하여 구하기도 하며 이를 중심 차분 또는 중앙 차분이라고 합니다.
- 진정한 미분 접선 과 수치 미분 근사로 구한 접선 의 값

- 미분의 나쁜 구현 예(문제점 2가지)
: 0.0이 답이 아닌데 출력되는 값이 0.0으로 출력됩니다.
import numpy as np
import matplotlib.pyplot as plt # 시각화 관련 패키지
# 미분의 나쁜 구현 예(문제점 2가지)
def numerical_diff(f, x):
h = 10e-50 # 1번째 문제점) 0에 최대한 가깝게 구현.
# But python의 경우 np.float32(1e-50)는 0.0으로 처리(반올림 오차)
return (f(x+h)-f(x)) / h # 2번째 문제점) 1e-50)보다 크게 하면 h에 의한 오차 발생.
def function_1(x):
return 0.01 * x ** 2 +0.1 * x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
# plt.show()
print(numerical_diff(function_1,5))
출력값 : 0.0
- 문제점 해결 수치 미분의 예
: 중앙차분 , 오차를 줄일 수 있도록 합니다(반드시 오차가 줄어드는 것은 아닙니다).
def numerical_diff(f,x):
h = 1e-4 # 0.0001
return (f(x+h) -f(x-h))/2*h
# x를 중심으로 그 전후의 차분을 계산한다. : 중심차분 혹은 중앙차분
# 오차는 존재하지만 접선의 기울기를 그리는 것과 같은 효과를 낼 수 있다.
def function_1(x):
return 0.01 * x ** 2 +0.1 * x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
# plt.show()
print(numerical_diff(function_1,5))
# 1.9999999999908982e-09
편미분
: 변수가 여러 개인 함수에 대한 미분을 편미분이라고 합니다. 편미분 역시 변수가 하나인 미분과 동일하게 특정 장소에 대한 기울기를 구합니다. 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정합니다.

# - f(x0,x1) = x0**2 + x1**2
def function_2(x):
return x[0]**2 + x[1]**2
# 또는 return np.sum(x ** 2)
# x0 = 3, x1 = 4 일때, x0에 편미분
def function_tmp1(x0):
return x0 * x0 + 4.0 ** 2.0
# x0 = 3, x1 = 4 일때, x1에 편미분
def function_tmp2(x1):
return 3 * 2 + x1 * x1
print(numerical_diff(function_tmp1,3))
# 수치미분값(편미분) - x0 출력값 : 6.000000000003781e-08
print(numerical_diff(function_tmp2,4))
# 수치미분값(편미분) - x1 출력값 : 7.999999999999119e-08
기울기 (Grandient)
: 모든 변수의 편미분을 벡터로 정리한 것을 기울기 gradient라고 합니다. 기울기는 가장 낮은 장소를 가리키지만 각 지점에서 낮아지는 방향을 의미합니다. 기울기가 가리키는 쪽은 각 장소에서 함수의 출력 값을 가장 줄이는 방향이라고 할 수 있습니다.

모든 변수의 편미분을 동시에 계산하고 싶다을 때
양쪽의 편미분을 묶어서 계산 합니다.
경사하강법
: 손실함수를 기준으로 오차값을 보고 음수쪽으로 이동할지 양수쪽으로 이동할지를 판단합니다. 손실합수의 접선의 기울기를 구하여 양수가 나오면 음수를 넣어주고, 음수가 나오면 양수를 넣어줘서 접선의 기울기가 0이 나오도록 합니다. 손실을 최소화 하는 값을 추적해가는 알고리즘입니다.
- 기울기를 잘 이용해 함수의 최소값 또는 가능한 한 작은 값 을 찾으려는 것 이 경사 하강법
- 접선의 기울기가 0이 되는 지점이 최소값이 됩니다(음수가 나오면 양수로 이동 , 양수가 나오면 음수가 나오도록
값을 조정합니다).

학습률 = 얼마 만큼 이동(간격)할 것인가? 값을 넣어주는 것은 분석하는 사람의 역할입니다.
import numpy as np
import matplotlib.pyplot as plt
# 경사하강법 (손실을 최소화)
def numerical_gradient_no_batch(f,x):
# 배치단위가 아닌 미분 값을 구현되어지게 만듦. - 중앙차분(미분)
h = 1e-4
grad = np.zeros_like(x)
# _like를 가진 함수의 공통점 : _like(배열) 지정한 배열과 동일한 shape의 행렬을 만듦
# 입력으로 전달되는 shape 과 같은 shape를 초기값을 0으로 생성
for idx in range(x.size):
tmp_val = x[idx] # x값을 꺼내와서 변수에 담아주었다.
# f(x+h) 계산
x[idx] = float(tmp_val) + h
fxh1 = f(x)
# f(x-h) 계산
x[idx] = float(tmp_val) - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2 * h) # 중앙차분
x[idx] = tmp_val
return grad
def numerical_gradient(f,x): # 편미분 정의 함수 (함수,입력값(단항,다항))
if x.ndim == 1 : # 단항
return numerical_gradient_no_batch(f,x)
else:
grade = np.zeros_like(x)
# _like를 가진 함수의 공통점 : _like(배열) 지정한 배열과 동일한 shape의 행렬을 만듦
# 입력으로 전달되는 shape 과 같은 shape를 초기값을 0으로 생성
for idx, z in enumerate(x):
# enumerate() : 입력으로 전달 받은 값을 자돟으로 인덱스 값을 0부터 증가하면서 x의 담긴 값을 반환
grade[idx] = numerical_gradient_no_batch(f, x)
return grade
def gradient_descent(f, init_x, lr, step_num): # 함수, 초기값, learning rate, 횟수 - 경사하강법
x = init_x # 초기값
x_history = [] # 학습을 통해서 나온 값들을 저장하여, 시각화 할 때 사용
for i in range(step_num): # 20번 반복
x_history.append(x.copy()) # 초기값을 가져와 저장한 이후 입력으로 전달되는 데이터 추가.
grad = numerical_gradient(f,x) # 편미분
x -= lr * grad
return x, np.array(x_history) # 반복이 끝난 이후!!!!
# 튜플의 가로 생략 된것이지 2개가 return이 되는 것이 아니다.
def function_2(x): # f(x0, x1) = x0^2 + x1^2
return x[0]**2 + x[1]**2
if __name__ =="__main__":
init_x = np.array([-3.0, 4.0])
# 초기값 셋팅(내부에서 처리 될 때, float으로 처리 되기 때문에 float형(실수)로 넣어줘야한다.
lr = 0.1 # learning rate(학습률)
step_num = 20 # 경사하강법의 학습을 시킬 때, 학습시킬 횟수의 값(20회)
x, x_history = gradient_descent(function_2, init_x, lr, step_num)
# 함수, 초기값, learning rate, 회수 / 튜플로 반환해서 튜플로 받은 것(변수 2개x)
plt.plot([-5,5],[0,0],'--b')
plt.plot([0, 0], [-5, 5], '--b')
plt.plot(x_history[:,0], x_history[:,1], 'o')
plt.xlim(-3.5, 3.5)
plt.ylim(-4.5, 4.5)
plt.xlabel("X0")
plt.ylabel("X1")
plt.show()
f(x0, x1) = x0^2 + x1^2

경사하강법을 이용하여 (0.0)으로 조정
신경망에서의 기울기
- 가중치 매개변수에 대한 손실 함수의 기울기
- 예 ) 형상이 2 x 3, 가중치 W, 손실 함수 L 인 신경망의 경우
각각을 독립적으로 편미분으로 수행되어지게 만들주면 최소가 되도록 만들어줍니다.
'Anaconda > DeepLearning' 카테고리의 다른 글
| [DeepLearning] 오차역전파법 (backpropagation) (0) | 2020.08.10 |
|---|---|
| [DeepLearning] 확률적 경사 하강법(SGD), 학습 알고리즘 구현 (0) | 2020.08.07 |
| [DeepLearning] 신경망(neural network) (0) | 2020.08.04 |
| [DeepLearning] 넘파이(NumPy) (0) | 2020.08.03 |
| [DeepLearning] 퍼셉트론(perceptron) (0) | 2020.08.03 |




