Practice makes perfect
[DeepLearning] 확률적 경사 하강법(SGD), 학습 알고리즘 구현 본문
확률적 경사 하강법 (Stochastic Gradient Descent, SGD)
: 데이터를 미니배치로 무작위로 선정하여 경사 하강법으로 매개변수를 갱신하는 방법으러 추출된 데이터 한개에 대해서 그래디언트를 계산하고, 경사 하강 알고리즘을 적용합니다.
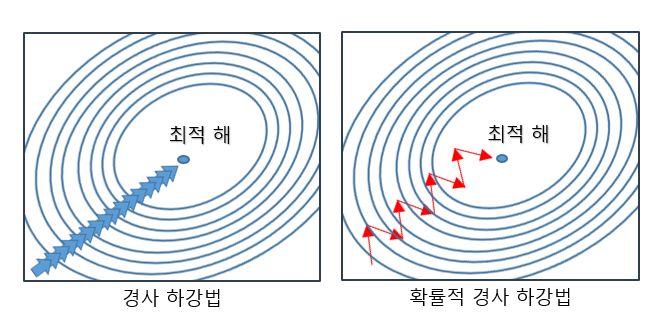
+) 추출된 데이터 한 개에 대해서 error gradient 를 계산하고, Gradient descent 알고리즘을 적용하는 방법
모델의 레이어 층은 하나의 행렬곱으로 생각할 수 있고, 여러개의 묶음 데이터는 행렬이라고 생각 할 수 있습니다.
즉, 여러개의 묶음 데이터를 특정 레이어 층에 입력하는 것은 행렬 x 행렬로 이해할 수 있는데, SGD는 입력 데이터 한 개만을 사용하기 때문에 한 개의 데이터를 '벡터' 로 표현하여 특정 레이어 층에 입력하는 것으로 이해할 수 있고 이는 벡터 x 행렬 연산이 됩니다.
- 전체 데이터를 사용하는 것이 아니라, 랜덤하게 추출한 일부 데이터를 사용한느 것입니다.. 따라서 학습 중산 과정에서 결과의 진폭이 크고 불안정하며, 속도가 매우 빠릅니다. 또한 데이터 하나씩 처리하기 때문에 오
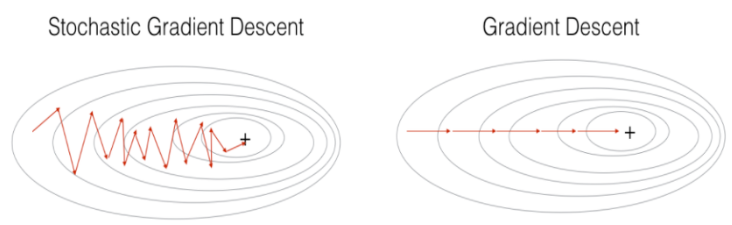
SGD 장점
- 위 그림에서 보이듯이 Shooting 이 일어나기 때문에 local optimal 에 빠질 리스크가 적다.
- step 에 걸리는 시간이 짧기 때문에 수렴속도가 상대적으로 빠르다.
SGD의 단점
- global optimal 을 찾지 못 할 가능성이 있다(오차율이 크다)
: 단점을 보완하기 위해 Mini batch를 이용한 방법이며, 활률적 경사 하강법의 노이즈를 줄이면서도 전체 배치보다
더 효율적으로 수행할 수 있습니다.
- 데이터를 한개씩 처리하기 때문에 GPU의 성능을 전부 활용할 수 없다.
신경망 학습 절차
전제 - 학습
: 가중치와 편향을 훈련 데이터에 적응하도록 조정하는 과정
1 단계 미니배치
: 훈련 데이터 중 일부를 무작위로 가져오는 미니배치를 통해 손실 함수 값을 줄이는 것이 목표
2 단계 기울기 산출
: 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구함 .
기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시함
3 단계 매개변수 갱신
: 가중치 매개변수를 기울기 방향으로 아주 조금 갱신함
4 단계 반복
: 1 ~ 3 단계를 반복함
신경망 설계 (전제 - 학습)
1) 생성자 생성
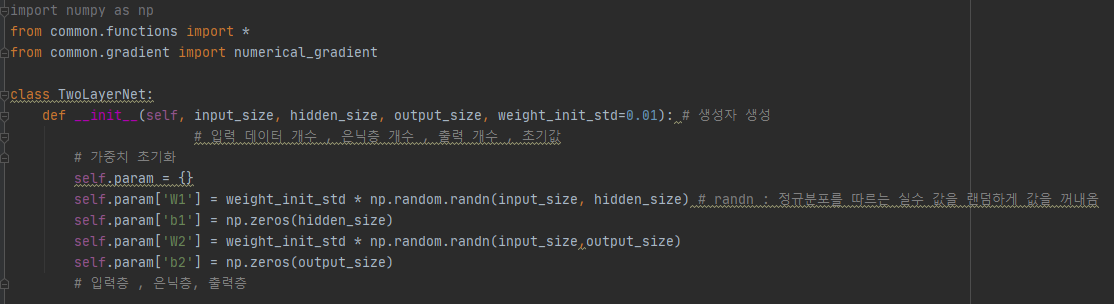
2) predict - 데이터의 흐름에 대한 기능 구현

3) 손실함수 활용(교차 엔트로피 오차)

4) 정확도 체크 함수 정의
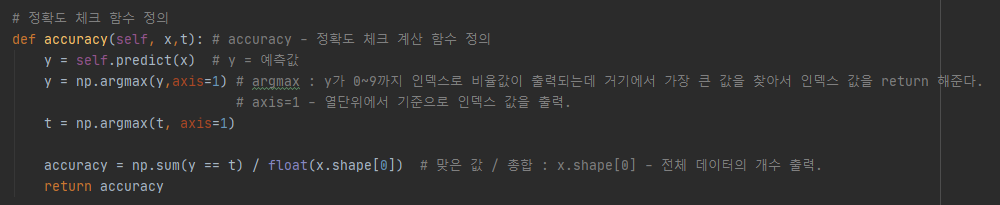
5) 경사하강법
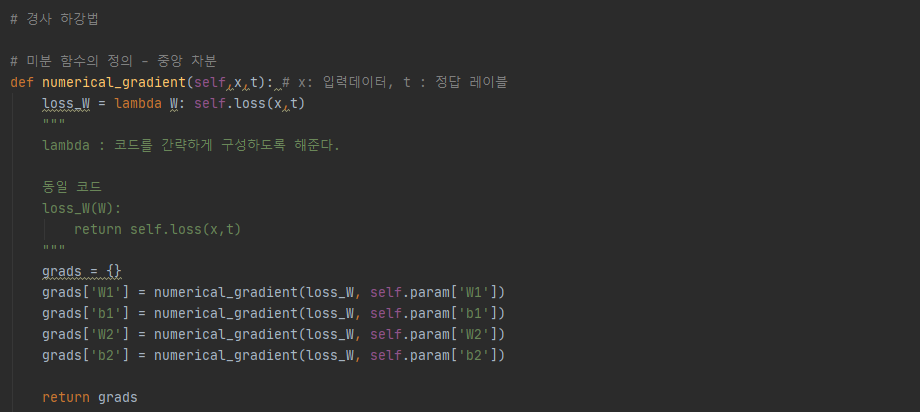
- common 밑에 있는 함수를 호출 한 것인데, 자신 안에 자신과 동일한 이름의 함수가 사용된다면 어떻게 구분할까?
: class 안의 함수나 메서드를 선어하려면 'self.' 을 붙여야지만 선언이 가능한데 같은 자료형 안이어도 'self.' 으로 호출해야지 내가 선언한 함수를 사용되므로 외부의 정의 되어 있는 함수를 찾아서 수행합니다.
신경망 실행 - 학습 시키기
: 위에서 설계한 신경망을 Mnist 데이터를 사용하여 실행하도록 하겠습니다.
1) 데이터 읽기
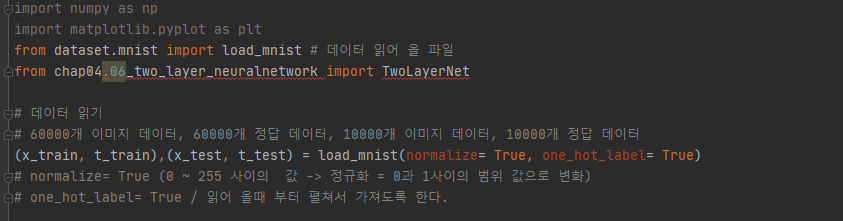
2) 인스턴스화

3) 하이퍼 파라미터

4) 학습하면서 나오는 손실값 - 값이 작아지는 것을 확인

5) 미니 배치 방식

6) 기울기 계산(미분)

7) 매개변수(가중치, 편향) 갱싱

8) 학습 경과 정확도 확인
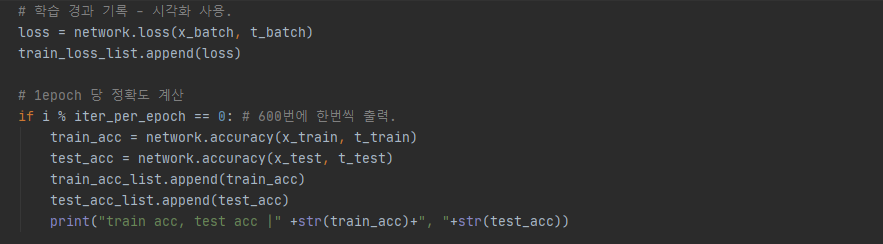
9) 시각화


'Anaconda > DeepLearning' 카테고리의 다른 글
| [DeepLearning] 합성곱 신경망 (Convolutional Neural Network, CNN) (0) | 2020.11.20 |
|---|---|
| [DeepLearning] 오차역전파법 (backpropagation) (0) | 2020.08.10 |
| [DeepLearning] 신경망 학습 (0) | 2020.08.06 |
| [DeepLearning] 신경망(neural network) (0) | 2020.08.04 |
| [DeepLearning] 넘파이(NumPy) (0) | 2020.08.03 |




