Practice makes perfect
[R] 비지도 학습의 방법 : 군집분석(Clustering Analysis) 본문
비지도 학습(Unsupervised Learning)
: 사람 없이 컴퓨터가 스스로 레이블 되어 있지 않은 데이터에 대해 학습하는 것으로 y없이 x만 이용해서 학습하는 것 입니다. 정답이 없는 문제를 푸는 것이므로 학습이 맞게 됐는지 확인할 길은 없지만, 인터넷에 있는 거의 모든 데이터가 레이블이 없는 형태로 있으므로 앞으로 기계학습이 나아갈 방향으로 설정되어 있습니다. 통계학의 군집화와 분포 추정 등의 분야와 밀접한 관련이 있습니다.
– 컴퓨터 기계학습에 의한 분석 방법
– 종속변수(y) 없음 : 입력 데이터에 정답 없음
– 분석방법 : 규칙(패턴분석) → 공학.자연과학 계열(100년)
– 분석유형 : 연관분석, 군집분석 → 데이터마이닝 기반
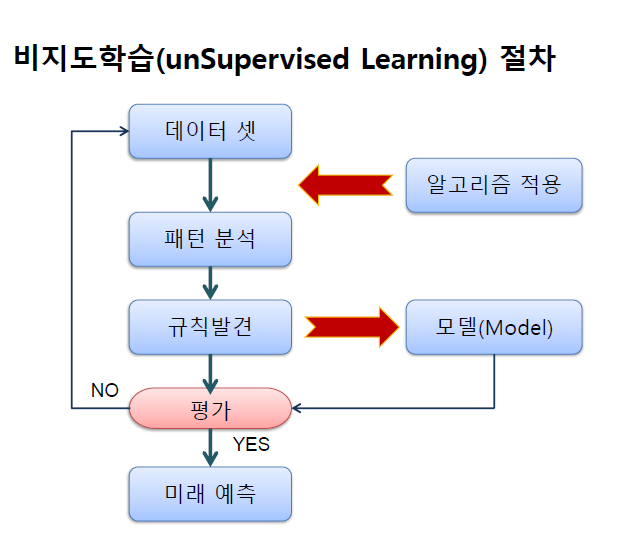
군집화(Clustering) - 군집분석(Clustering Analysis) : 그룹화를 통한 예측(그룹 특성 차이 분석-고객집단 이해)
: 데이터가 쭉 뿌려져 있을 때 레이블이 없다고 해도 데이터간 거리에 따라 대충 두 세개의 군집으로 이렇게 x만 가지고 군집을 학습하는 것을 군집화 라고 합니다.
군집 분석
– 종속변수(y변수)가 없는 데이터 마이닝 기법
– 유클리드 거리 기반 유사 객체 묶음
– 고객 DB -> 알고리즘 적용 -> 패턴 추출(rule) -> 근거리 모형으로 군집형성
– 계층적 군집분석(탐색적), 비계층적 군집분석(확인적)
– 주요 알고리즘 : k-means, hierarchical
군집분석 특징
– 전체적인 데이터 구조를 파악하는데 이용
– 관측대상 간 유사성을 기초로 비슷한 것 끼리 그룹화(Clustering)
– 유사성 = 유클리드 거리
유크리드 거리
: 유클리디안 거리(Euclidean distance)는 두 점 사이의 거리를 계산하는 방법으로, 이 거리를 이용하여 유클리드 공간을 정의
유클리드 거리 계산식
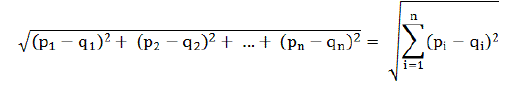
관측대상 p와 q의 대응하는 변량값의 차가 작으면, 두 관측대상은 유사하다고 정의하는 식
– 분석결과에 대한 가설 검정 없음(타당성 검증 방법 없음)
– 분야 : 사회과학, 자연과학, 공학 분야
– 척도 : 등간, 비율척도(연속적인 양)
군집 구성법
– 그룹간의 유사성 계산 방법
– 최단거리법, 최장거리법, 메디안법, 중심법, 그룹평균법
군집화방법
– 계층 군집화 : 가장 가까운 대상끼리 순차적으로 묶음
– 비계층 군집화 : k-평균 군집법
1. 유클리디안 거리
실습) 유클리디안 거리 계산법
① matrix 객체 생성
x <- matrix(1:9, nrow=3, byrow = T) # nrow=3 : 3행으로 만듬, byrow = T : 열 중심 -> 행 중심
x
- 출력값 -
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
② 유클리디안 거리 생성
dist <- dist(x, method="euclidean") # method 생략가능 / euclidean : 유클리디안 거리 생성
dist
- 출력값 -
1 2
2 5.196152
3 10.392305 5.196152
5.196152 : 전체 루트 (2행 - 1행 = x^2 + 2행 - 1행 = x^2 + 2행 - 1행 = x^2)
10.392305 : 전체 루트 (3행 - 1행 = x^2 + 3행 - 1행 = x^2 + 3행 - 1행 = x^2)
5.196152 : 전체 루트 (3행 - 2행 = x^2 + 3행 - 2행 = x^2 + 3행 - 2행 = x^2)
③ 유클리드 거리 계산식의 R코드
# 1행과 2행 변량의 유클리드 거리 구하기
sqrt(sum((x[1,] - x[2, ])^2)) 출력값 : 5.196152
# 1행과 3행 변량의 유클리드 거리 구하기
sqrt(sum((x[1,] - x[3, ])^2)) 출력값 : 10.3923
2. 계층적 군집분석(탐색적 분석)
실습) 유클리디안 거리를 이용한 군집화
① 군집분석(Clustering)분석을 위한 패키지 설치
install.packages("cluster")
library(cluster)
② 데이터 셋 생성
x <- matrix(1:9, nrow=3, by=T)
x
- 출력값 -
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 4 5 6
[3,] 7 8 9
③ matrix 대상 유클리드 거리 생성 함수
dist <- dist(x, method="euclidean") # method 생략가능
dist
- 출력값 -
1 2
2 5.196152
3 10.392305 5.196152
④ 유클리드 거리 matrix를 이용한 클러스터링
hc <- hclust(dist) # 클러스터링 적용
hc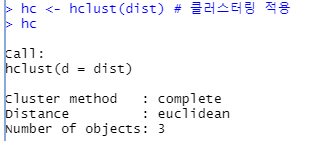
⑤ 클러스터 시각화
x11()
plot(hc) # 1과2 군집(클러스터) 형성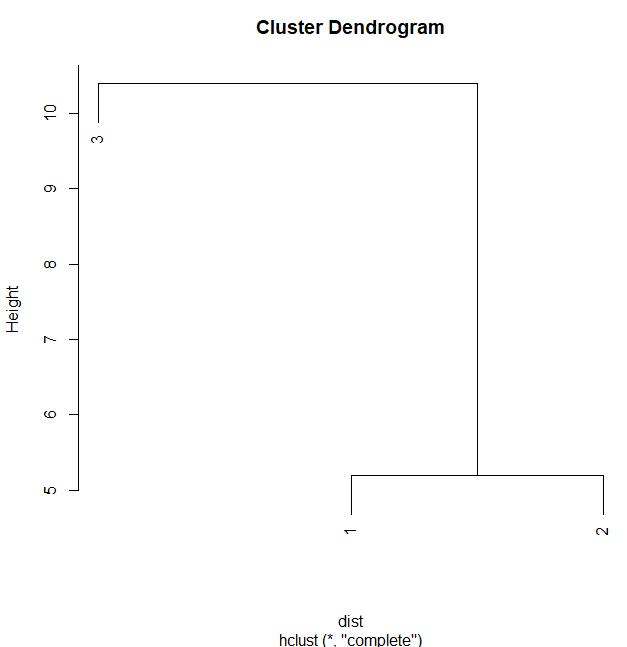
- 1 과 2 는 같은 레벨임을 보여주고, 3번은 값의 차이가 월등히 높음을 보여줍니다.
- 1 과 2 유사성을 가진 가까운 것 먼저 그룹핑을 해줍니다.
실습) 신입사원 면접시험 결과 군집분석
① 데이터 셋 가져오기
interview <- read.csv("interview.csv", header=TRUE)
names(interview)
- 출력값 -
[1] "no" "가치관" "전문지식" "발표력" "인성" "창의력" "자격증" "종합점수"
[9] "합격여부"
View(interview)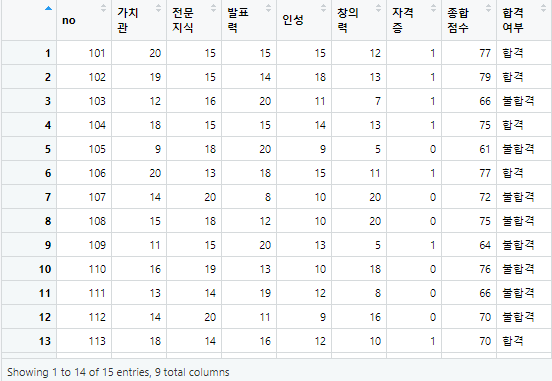
② 유클리디안 거리 계산
interview_df <- interview[c(2:7)] # 2~7 열까지만 선택(가치관~자격증 점수)
idist<- dist(interview_df) # no, 종합점수, 합격여부 제거
head(idist) 출력값 : [1] 3.464102 11.445523 2.449490 15.524175 3.741657 14.142136
③ 계층적 군집분석
hc <- hclust(idist)
hc
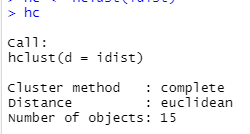
15개의 object 유클리드 거리법으로 출력
④ 군집분석 시각화
x11()
plot(hc, hang=-1) # 덴드로그램에서 음수값을 제거할 수 있음.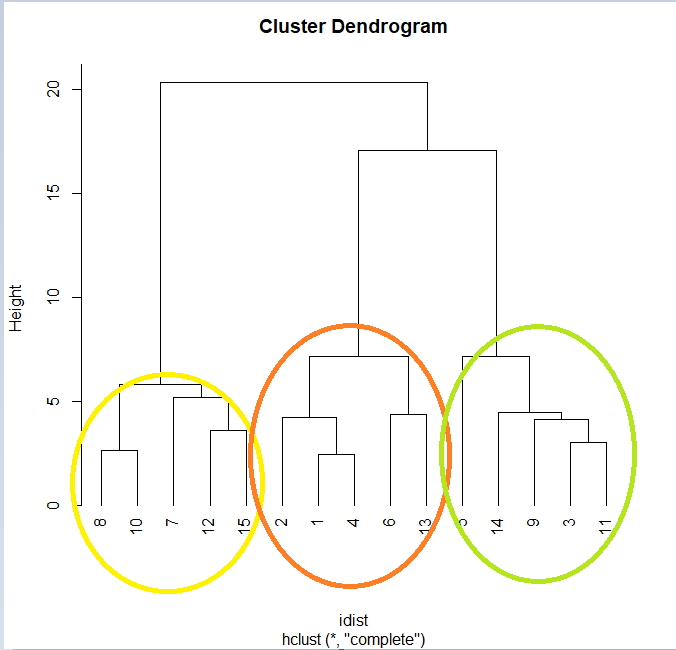
거리의 계산을 통해서 크기의 값을 시각화해서 보여주는데 15개를 어떻게 군집화 할 수 있을지 보여주고 있습니다.
⑤ 군집 단위 테두리 생성
rect.hclust(hc, k=3, border="red") # 3개 그룹 선정, 선 색 지정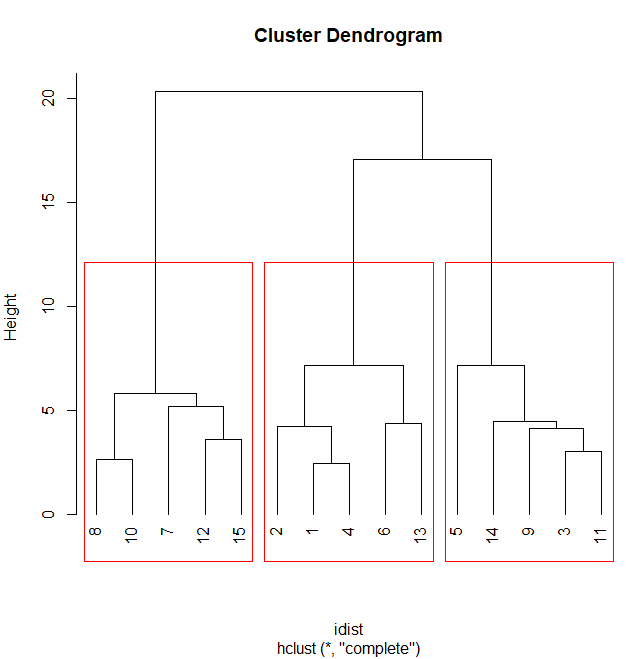
위의 결과를 통해서 예상했던 결과가 추가적인 코드를 통해서 출력되었습니다.
실습) 군집별 특징 보기
① 각 그룹별 서브셋 만들기
g1<- subset(interview, no==108| no==110| no==107| no==112 | no==115)
g2<- subset(interview, no==102| no==101| no==104| no==106 | no==113)
g3<- subset(interview, no==105| no==114| no==109| no==103 | no==111)
② 그룹 요약통계량 - 공통점 : 자격증
summary(g1) # 불합격:5, 자격증 없음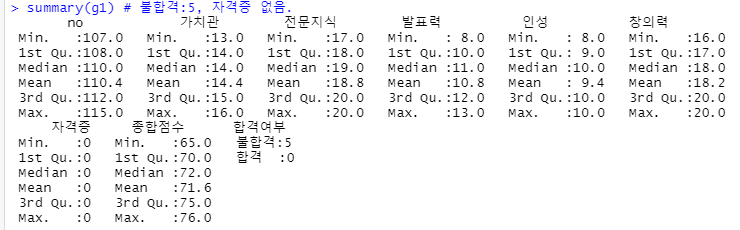
summary(g2) # 합격:5, 자격증 있음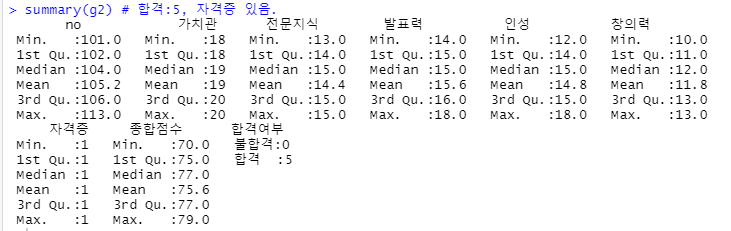
ummary(g3) # 불합격:5, 자격증 없음+있음.
table(g3$자격증)
- 출력값 -
0 1
3 2
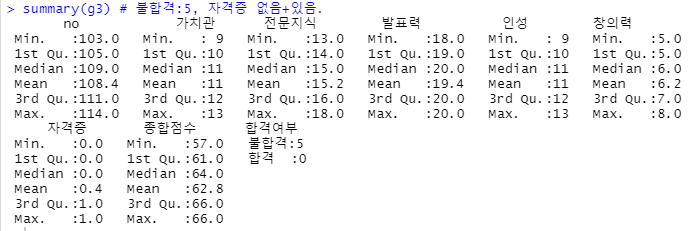
- 자격증을 가지고 있어도 불합격 하는 사람들이 존재합니다.
3. 군집 수 자르기
실습) iris 데이터 셋을 대상으로 군집 수 자르기
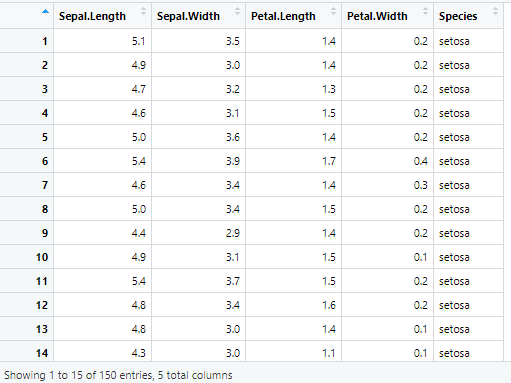
iris 데이터 셋
iris 데이터 셋
R에서 제공되는 기본 데이터 셋으로 3가지 꽃의 종류별로 50개씩 전체 150개의 관측치로 구성된다. iris는 붓꽃에 관한 데이터를 5개의 변수로 제공하며, 각 변수의 내용은 다음과 같다.
Sepal.Length(꽃받침 길이)
Sepal.Width(꽃받침 너비)
Petal.Length(꽃잎 길이)
Petal.Width(꽃잎 너비)
Species(꽃의 종류) : 3가지 종류별 50개 (전체 150개 관측치)
① 유클리드안 거리 계산
idist<- dist(iris[1:4]) # dist(iris[, -5])
# 계층형 군집분석(클러스터링)
hc <- hclust(idist)
hc
plot(hc, hang=-1)
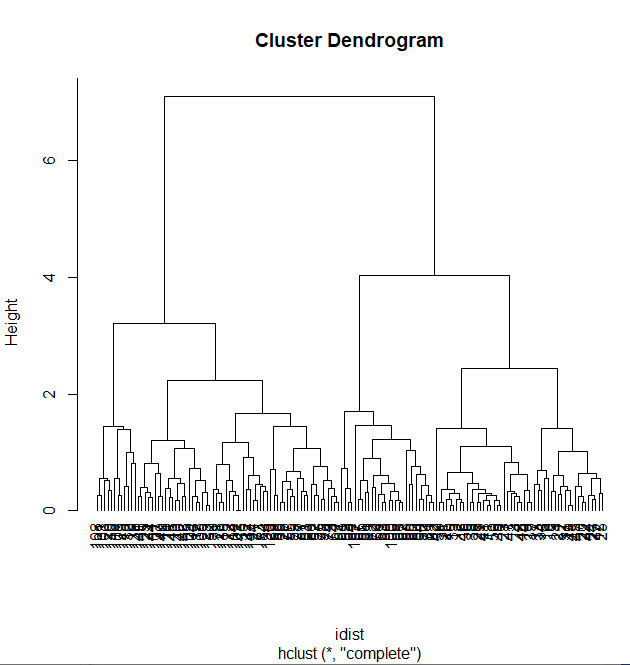
rect.hclust(hc, k=4, border="red") # 4개 그룹수
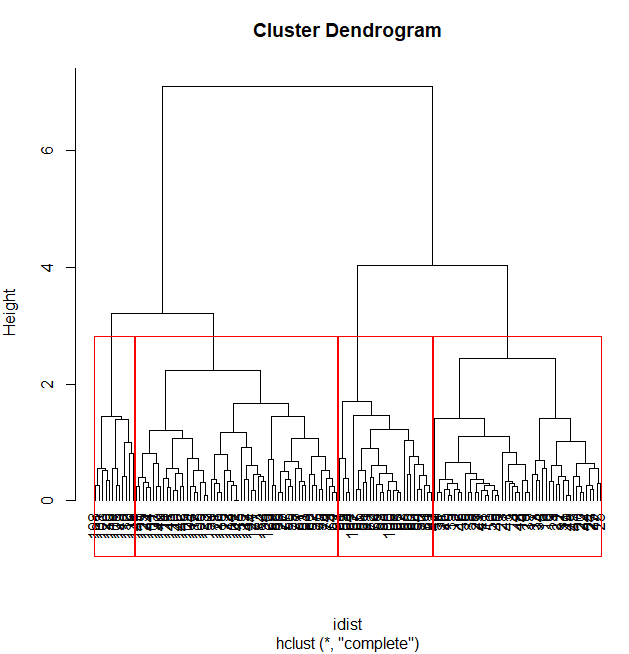
② 군집 수 자르기
ghc<- cutree(hc, k=3) # stats 패키지 제공 - 3개로 그룹핑
ghc # 150개(그룹을 의미하는 숫자(1~3) 출력)
③ iris에서 ghc 컬럼 추가
iris$ghc <- ghc
head(iris)
- 출력값 -
Sepal.Length Sepal.Width Petal.Length Petal.Width Species ghc
1 5.1 3.5 1.4 0.2 setosa 1
2 4.9 3.0 1.4 0.2 setosa 1
3 4.7 3.2 1.3 0.2 setosa 1
4 4.6 3.1 1.5 0.2 setosa 1
5 5.0 3.6 1.4 0.2 setosa 1
6 5.4 3.9 1.7 0.4 setosa 1
table(iris$ghc) # ghc 빈도수
- 출력값 -
1 2 3
50 72 28 
versicolor 와 virginica 의 돤벽하게 구분이 되지 않습니다. ( 공통 되어지는 부분 존재 )
④ 요약통계량 구하기
g1 <- subset(iris, ghc==1)
summary(g1[1:4])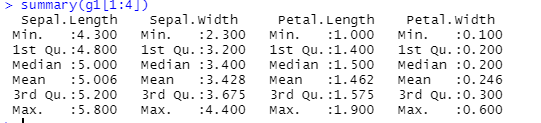
g2 <- subset(iris, ghc==2)
summary(g2[1:4])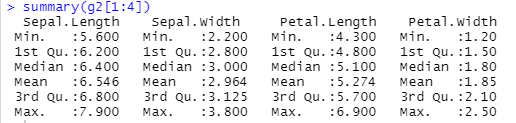
g3 <- subset(iris, ghc==3)
summary(g3[1:4])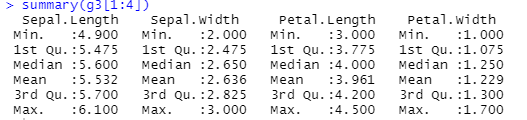
4. 비계층적 군집분석
: 데이터 셋을 대상으로 계층적으로 군집분석 시각화하는 군집 수를 파악한 후 k-means 알고리즘에 군집수를 적용하여 군집별로 시각화하는 방법
실습) ggplot2 패키지에서 제공되는 diamonds 데이터 사용
diamonds 데이터 셋
diamonds 데이터 셋
ggplot2 패키지에서 제공하는 데이터 셋으로, 약 5만4천개의 다이아몬드에 관한 속성을 기록한 데이터 셋으로 53,940개의 관측치와 10개의 변수로 구성되어 있다. 주요 변수에 대한 설명은 다음과 같다.
- 주요 변수 -
price : 다이아몬드 가격($326 ~ $18,823)
carat : 다이아몬드 무게(0.2 ~ 5.01)
cut : 컷의 품질(Fair, Good, Very Good, Premium, Ideal)
color : 색상(J : 가장 나쁨 ~ D : 가장 좋음)
clarity : 선명도(I1 : 가장 나쁨, SI1, SI2, VS1, VS2, VVS1, VVS2, IF : 가장 좋음)
x : 길이(0~10.74mm), y : 폭(0~58.9mm), z : 깊이(0~31.8mm),
depth : 깊이 비율 = z / mean(x, y)
① 군집분석에 사용할 변수 추출
install.packages("ggplot2", dependencies = T)
library(ggplot2)
data(diamonds)
dim(diamonds) 출력값 : [1] 53940 10
t <- sample(1 : nrow(diamonds),1000) # 1000개 데이터 샘플링
test <- diamonds[t, ] # 1000개 표본 추출
dim(test) 출력값 : 1000 10
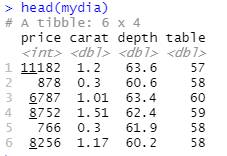
head(test) # 검정 데이터
mydia <- test[c("price","carat", "depth", "table")] # 4개 칼럼만 선정
head(mydia)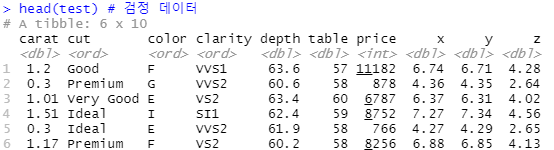
② 계층적 군집분석(탐색적 분석)
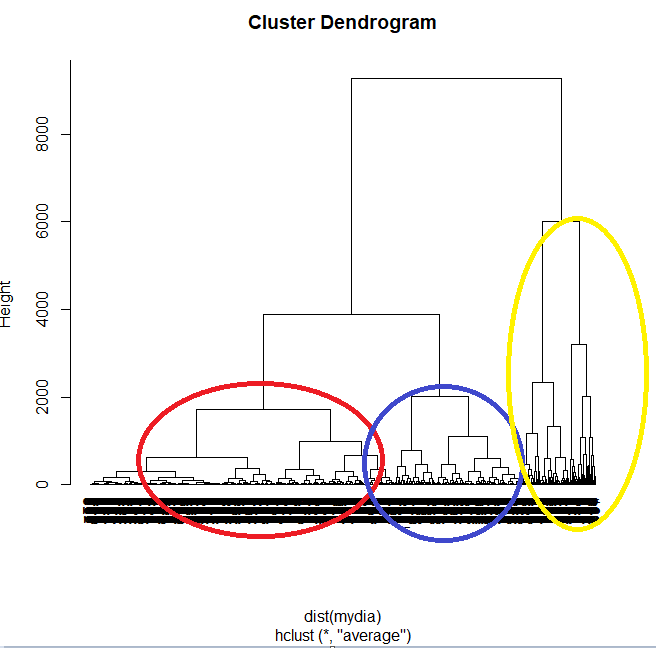
result <- hclust(dist(mydia), method="average") # 평균거리 이용
result
plot(result, hang=-1) # hang : -1 이하 값 제거
군집 방법(Cluster method)
method = "complete" : 완전결합기준(최대거리 이용) <- default(생략시)
method = "single" : 단순결합기준(최소거리 이용)
method = "average" : 평균결합기준(평균거리 이용)
③ 비계층적 군집분석
result2 <- kmeans(mydia, 3) # 3개 군집 수 적용.
names(result2) # cluster 칼럼 확인
- 출력값 -
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault"
result2$cluster # 각 케이스에 대한 소속 군집수(1,2,3)
result2$centers # 각 군집 중앙값
- 출력값 -
price carat depth table
1 5923.048 1.1164384 61.83801 57.79007
2 1579.091 0.5119504 61.60182 57.35521
3 13368.243 1.7415534 61.93010 58.17476
# 원형데이터에 군집수 추가
mydia$cluster <- result2$cluster # 1 ~ 3 중 하나의 분주에 들어가 있음
head(mydia) # cluster 칼럼 확인 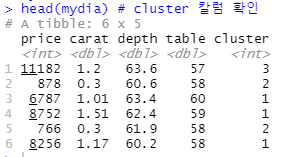
④ 변수 간의 상관계수 보기
cor(mydia[,-5], method="pearson") # 상관계수 보기
- 출력값 -
price carat depth table
price 1.00000000 0.91936804 0.06374813 0.09980938
carat 0.91936804 1.00000000 0.07630058 0.15321267
depth 0.06374813 0.07630058 1.00000000 -0.25949149
table 0.09980938 0.15321267 -0.25949149 1.00000000
plot(mydia[,-5])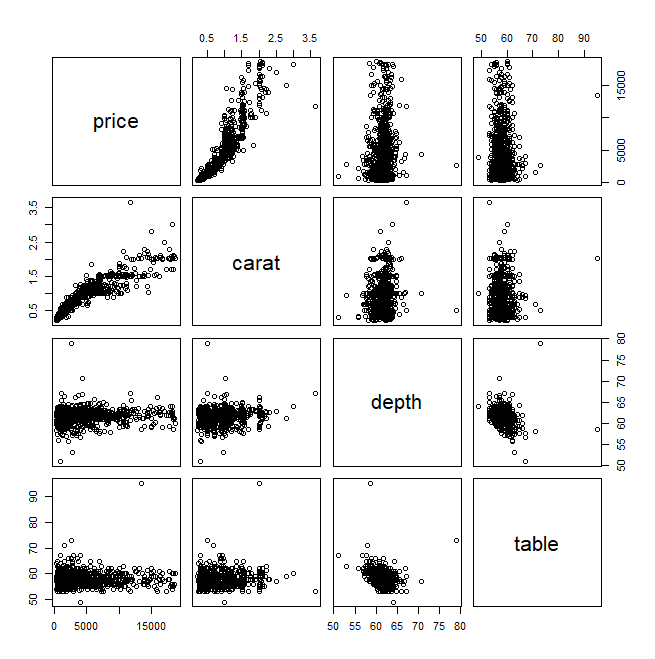
- 상관계수 색상 시각화
install.packages('mclust')
install.packages('corrgram')
library(mclust)
library(corrgram) # 상관성 시각화
corrgram(mydia[,-5]) # 색상 적용 - 동일 색상으로 그룹화 표시
corrgram(mydia[,-5], upper.panel=panel.conf) # 수치(상관계수) 추가(위쪽)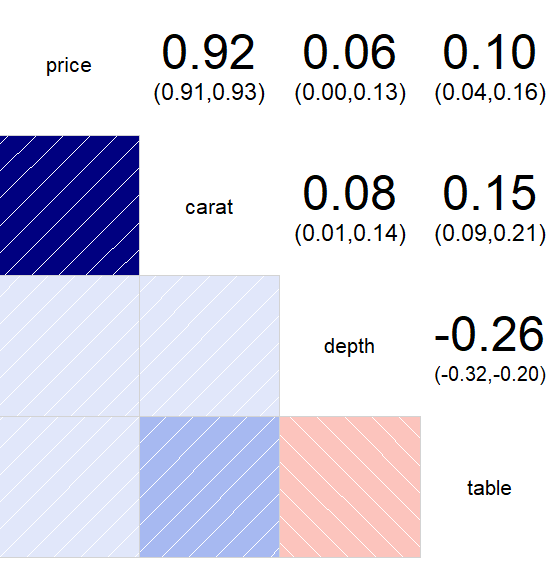
⑤ 비계층적 군집시각화
plot(mydia$carat, mydia$price, col=mydia$cluster)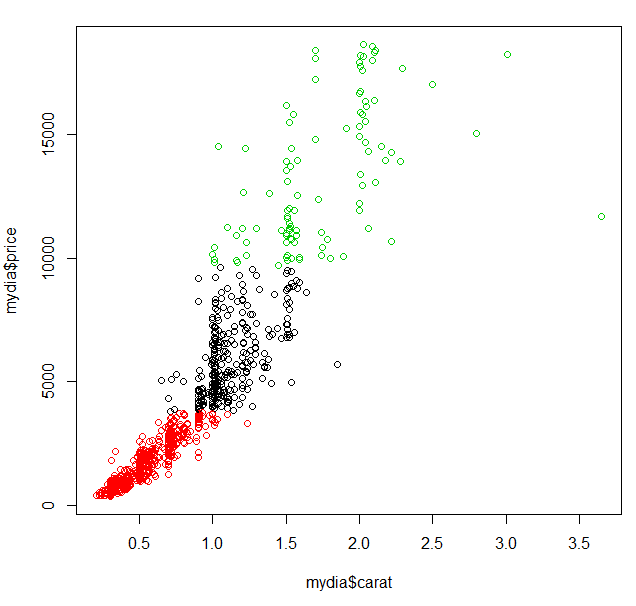
- 중심점 표시 추가
points(result2$centers[,c("carat", "price")], col=c(3,1,2), pch=8, cex=5)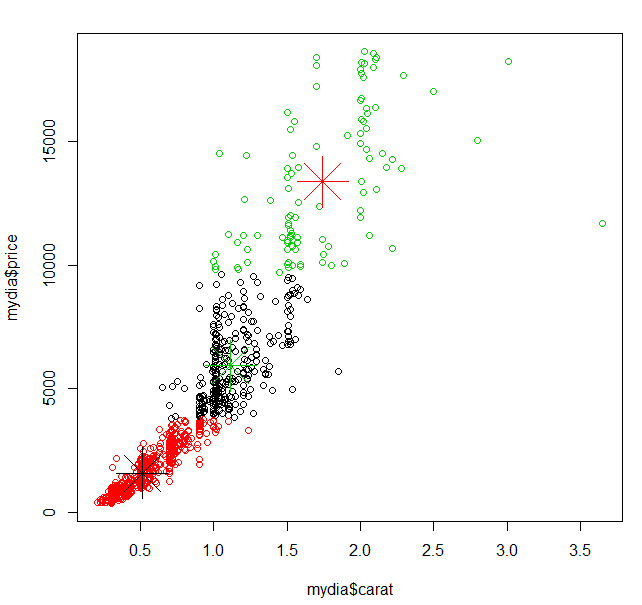
'빅데이터 > R' 카테고리의 다른 글
| [R] 시계열 분석(Timeseries Analysis) (7) | 2020.07.22 |
|---|---|
| [R] 비지도 학습의 방법 : 연관분석 (Association Analysis) (1) | 2020.07.22 |
| [R] 지도학습의 방법 : 분류분석(Classification) (0) | 2020.07.20 |
| [R] 지도학습의 방법 : 회귀분석(Regression Analysis) (0) | 2020.07.17 |
| [R] 머신러닝(Machine Learning) (0) | 2020.07.17 |




