Practice makes perfect
[R] 지도학습의 방법 : 분류분석(Classification) 본문
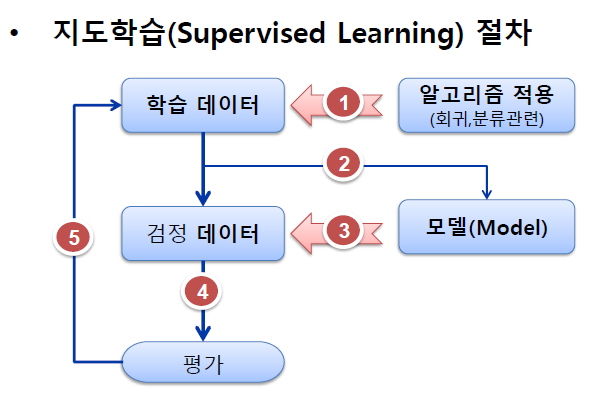
지도학습(Supervised Learning)
– 인간 개입에 의한 분석 방법
– 종속 변수(y) 존재 : 입력 데이터에 정답 포함
– 분석 방법 : 가설검정(확률/통계) → 인문.사회.심리 계열(300년)
– 분석 유형 : 회귀분석, 분류분석, 시계열 분석 → 추론통계 기반
분류분석(Decision Tree)
: 다수의 속성(attribute) 또는 변수를 갖는 객체를 사전에 정해진 그룹 또는 범주(class, category) 중의 하나로 분류하여 분석하는 방법입니다.
- 의사결정나무 (Decision Tree)
: 분류 모델링에 의해서 만들어진 규칙(rule)를 나무 모양으로 그리는 방법으로, 의사결정이 이뤄지는 시점과 성과를 한눈에 볼 수 있습니다.
의사결정나무(Decision Tree) 활용
- 세분화/분류 : 데이터를 비슷한 특성을 갖는 몇 개의 그룹 또는 몇 개의 등급으로 분할
- 예측 : 데이터에서 규칙을 찾아낸 후 이를 이용하여 미래의 사건을 예측
- 차원 축소 및 변수 선택 : 목표 변수에 큰 영향을 미치는 변수를 골라냄
- 변수들 간의 교호작용 (interaction effect) 파악 - 목표 변수의 범주를 병합하거나 연속형 목표 변수를 이산화(binning)
- 활용분야 고객을 분류하는 변수, 규칙, 특성들을 찾아내고, 이를 토대로 미래 잠재 고객의 행동이나 반응을 예측하거나 유도하는데 활용
의사결정나무(Decision Tree) 특징
- 결과를 설명하기 쉽다.
- 모형을 만드는 방법이 계산적으로 복잡하지 않다.
- 대용량 데이터도 빠르게 처리할 수 있다.
- 비정상 잡음 데이터에 대해서 민감하지 않다.
- 불필요한 변수가 있어도 크게 영향받지 않는다.
의사결정나무(Decision Tree) 알고리즘
a. CART (Classification and Regression Tree)
- 가장 많이 활용되는 알고리즘.
- 목표 변수가 범주형, 연속형 모두 가능. 이진 분리.
- 불순도 측도는 범주형일 경우 지니 지수, 연속형인 경우 분산을 사용.
- 개별 입력변수 뿐만 아니라 입력변수들의 선형결합드 중에서 최적의 분리를 찾을 수 있다.
b. C4.5 & C5.0
- 다지 분리(multiple split) 가능.
- 명목형 목표 변수.
- 불순도 측도는 엔트로피 지수 사용.
c. CHAID (Chi-squared Automatic Interaction Detection)
- 적당한 크기에서 나무모형의 성장을 중지.
- 연속형 목표변수.
- 불순도 측도는 카이제곱 통계량 사용.
분류분석의 특징
- 종속변수(y변수) 존재
- 종속변수 : 예측에 Focus을 두는 변수
- 비모수 검정 : 선형성, 정규성, 등분산성 가정 필요없음
- 단점 : 유의수준 판단 기준 없음(추론 기능 없음)
- 규칙(Rule)을 기반으로 의사결정트리 생성
분류 분석 vs 군집 분석 - 분류 분석은 이미 각 계급(클러스터)이 어떻게 정의 되는지 알고 있음
분류분석 테스트 환경
– 전수 데이터를 대상으로 할 경우 error를 감안해서 학습데이터와 검정데이터로 분리 하여 테스트
– 학습데이터(전수데이터의 70%) -> 알고리즘 적용 -> rule 발견
– rule 적용 -> 검정데이터(전수데이터의 30%) -> 검정(validate)
표본의 통계량으로 모집단의 모수 추론 과정과 유사
| 구분 | 추론동계 | 데이터마이닝 |
| 데이터 | 표본 | 전수테이터 |
| 검정방법 | 통계량/추론 | Rule/검증 |
의․생명분야에서 분류분석 사례

< 실습내용 >
: iris 데이터셋의 4개변수(Sepal Length,Sepal Width,Petal Length,Petal Width)값에 따라서 꽃의 종류(Species)가 분류되는 과정 알아보기
< 테스트 환경 >
전수 데이터를 대상으로 할 경우 error를 감안해서 학습데이터와 검증데이터로 분리 하여 테스트 한다.
학습데이터(훈련데이터) - (70%) -> 알고리즘 적용
rule 추출 -> 검정 테스트 (30%) -> 확인(validate) 데이터
표본의 통계량으로 모집단의 모수 추론과 유사함
iris 데이터 셋
iris 데이터 셋
R에서 제공되는 기본 데이터 셋으로 3가지 꽃의 종류별로 50개씩 전체 150개의 관측치로 구성된다. iris는 붓꽃에 관한 데이터를 5개의 변수로 제공하며, 각 변수의 내용은 다음과 같다.
Sepal.Length(꽃받침 길이)
Sepal.Width(꽃받침 너비)
Petal.Length(꽃잎 길이)
Petal.Width(꽃잎 너비)
Species(꽃의 종류) : 3가지 종류별 50개 (전체 150개 관측치)

1. party 패키지 적용 분류분석
실습1 ctree 함수 이용 의사결정트리 생성하기
① part패키지 설치
install.packages("party")
library(party) # ctree() 제공
② airquality 데이터 셋 로딩
library(datasets)
str(airquality)
- 출력값 -
'data.frame': 153 obs. of 6 variables:
$ Ozone : int 41 36 12 18 NA 28 23 19 8 NA ...
$ Solar.R: int 190 118 149 313 NA NA 299 99 19 194 ...
$ Wind : num 7.4 8 12.6 11.5 14.3 14.9 8.6 13.8 20.1 8.6 ...
$ Temp : int 67 72 74 62 56 66 65 59 61 69 ...
$ Month : int 5 5 5 5 5 5 5 5 5 5 ...
$ Day : int 1 2 3 4 5 6 7 8 9 10 ...airqulity 데이터 셋
airquality 데이터 셋
airquality 데이터 셋은 R에서 기본으로 제공되는 데이터 셋으로 New York시의 대기에 대한 질을 측정한 데이터 셋이다. 전체 153개의 관측치와 6개의 변수로 구성되어 있다.
주요 변수:
Ozone(오존 수치)
Solar.R(태양열)
Wind(바람)
Temp(온도)
Month(측정 월 5~9)
Day( 측정 날짜 1~31 일
③ formula 생성
formula <- Temp ~ Solar.R + Wind + Ozone
종속변수 : 온도, 독립변수 : 태양열, 바람, 오존 수치
④ 분류모델 생성 : formula를 이용하여 분류모델 생성
air_ctree <- ctree(formula, data=airquality)
air_ctree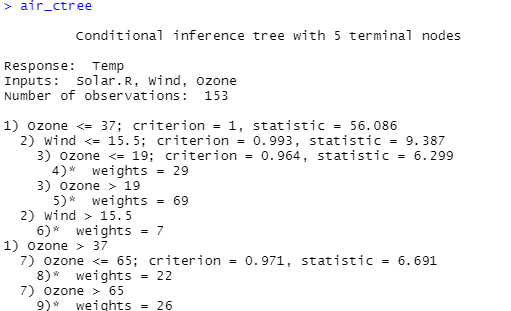
⑤ 분류분석 결과
plot(air_ctree)
오존 수치가 가장 많은 영향을 준다
1) 오존 37 이상
- 오존 65 이상 : Node 9
- 오존 65 이하 : Node 8
2) 오존 37 이하는 바람의 영향을 받음.
- 바람 15.5 이상 : Node 6
3) 바람 15.5 이하는 오존의 영향을 받음.
- 오존 19 이상 : Node 5
- 오존 19 이하 : Node 4
- 분류조건 subset 작성/확인
result <- subset(airquality, Ozone <= 37 & Wind > 15.5) # 오존 수치: 37 미만, 바람: 15.5 이상
summary(result$Temp)
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max.
57.0 61.0 63.0 65.2 72.0 73.0
실습2 학습데이터와 검정데이터 샘플링으로 분류분석하기
① 학습데이터와 검증데이터 샘플링
set.seed(1234) # 메모리에 시드값 적용 - 동일값 생성
idx <- sample(1:nrow(iris), nrow(iris) * 0.7)
train <- iris[idx,] # 70프로
test <- iris[-idx,] # 30프로
iris 데이터 셋
iris 데이터 셋
R에서 제공되는 기본 데이터 셋으로 3가지 꽃의 종류별로 50개씩 전체 150개의 관측치로 구성된다. iris는 붓꽃에 관한 데이터를 5개의 변수로 제공하며, 각 변수의 내용은 다음과 같다.
Sepal.Length(꽃받침 길이)
Sepal.Width(꽃받침 너비)
Petal.Length(꽃잎 길이)
Petal.Width(꽃잎 너비)
Species(꽃의 종류) : 3가지 종류별 50개 (전체 150개 관측치)

② formula 생성
-> 형식) 변수 <- 종속변수 ~ 독립변수
formula <- Species ~ Sepal.Length+Sepal.Width+Petal.Length+Petal.Width
③ 학습데이터 이용 분류모델 생성(ctree()함수 이용)
iris_ctree <- ctree(formula, data=train) # 학습데이터로 분류모델(tree) 생성
iris_ctree # Petal.Length,Petal.Width 중요변수

④ 분류모델 플로팅
plot() 이용 - 의사결정 트리로 결과 플로팅
plot(iris_ctree, type="simple")

plot(iris_ctree) # 의사결정트리 해석
종은 3개인데 결과가 4갱인 이유
Node 2 , Petal.Length 1.9 이하 = setosa
Node 5, Petal.Length 1.9 이상, Petal.Width 1.6이하, Petal.Length 4.6 이하 = versicolor
Node 6, Petal.Length 1.9 이상, Petal.Width 1.6이하, Petal.Length 4.6 이상 = versicolor or virginica (불명확)
Node 7, Petal.Length 1.9 이상, Petal.Width 1.6이상 = virginica
result <- subset(train, Petal.Length > 1.9 & Petal.Width <= 1.6 & Petal.Length > 4.6)
result$Species
- 출력값 -
virginica versicolor versicolor versicolor virginica versicolor virginica versicolor
Levels: setosa versicolor virginica
length(result$Species) 출력값 : 8
table(result$Species)
- 출력값 -
setosa versicolor virginica
0 5 3
⑤ 분류 모델 평가
모델 예측치 생성과 혼돈 매트릭스 생성
pred <- predict(iris_ctree, test) # 45
pred # Y변수의 변수값으로 예측
- 출력값 -
[1] setosa setosa setosa setosa setosa setosa setosa setosa
[9] setosa setosa setosa setosa setosa setosa setosa setosa
[17] versicolor versicolor versicolor versicolor versicolor versicolor versicolor versicolor
[25] versicolor virginica versicolor versicolor versicolor versicolor versicolor versicolor
[33] virginica virginica versicolor virginica virginica virginica virginica virginica
[41] virginica virginica virginica virginica virginica
Levels: setosa versicolor virginica
table(pred, test$Species)
- 출력값 -
pred setosa versicolor virginica
setosa 16 0 0 <- missing : 0
versicolor 0 15 1 <- missing : 1
virginica 0 1 12 <- missing : 1
분류정확도
(16+15+12) / nrow(test) 출력값 : 0.956
'빅데이터 > R' 카테고리의 다른 글
| [R] 비지도 학습의 방법 : 연관분석 (Association Analysis) (1) | 2020.07.22 |
|---|---|
| [R] 비지도 학습의 방법 : 군집분석(Clustering Analysis) (0) | 2020.07.21 |
| [R] 지도학습의 방법 : 회귀분석(Regression Analysis) (0) | 2020.07.17 |
| [R] 머신러닝(Machine Learning) (0) | 2020.07.17 |
| [R] 상관관계 분석(Correlation Analysis) (0) | 2020.07.17 |




