Practice makes perfect
[R] 지도학습의 방법 : 회귀분석(Regression Analysis) 본문
지도학습(Supervised Learning)
– 인간 개입에 의한 분석 방법
– 종속 변수(y) 존재 : 입력 데이터에 정답 포함
– 분석 방법 : 가설검정(확률/통계) → 인문.사회.심리 계열(300년)
– 분석 유형 : 회귀분석, 분류분석, 시계열 분석 → 추론통계 기반
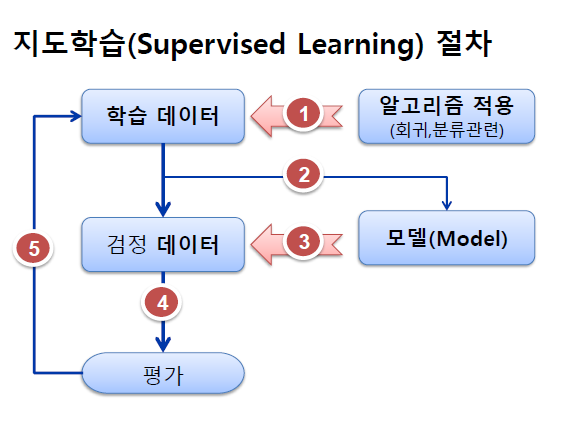
회귀분석(Regression Analysis) - 인과 관계
: 여러 자료들 간의 관계성을 수학적으로 추정, 설명한다. 흔히들 통계학의 꽃이라고 합니다. 독립변인이 종속변인에 영향을 미치는지 알아보고자 할 때 실시하는 분석 방법입니다. 선형 회귀법, 로지스틱 회귀법이 대표적이며, 로지스틱 회귀법을 앙상블했다는 관점으로 보면 인공신경망도 여기에 해당한다고 합니다. 선형 회귀법은 지도학습의 회귀문제를 푸는 데에 쓰이고(새로운 값의 예측), 로지스틱 회귀법과 인공신경망은 지도학습의 분류문제를 푸는데에 주로 사용합니다.
- 결과값을 알려주고, 가설을 일차 함수로 정의한 것으로 데이터(독립변수)를 넣어서 분석 시킴
ex) y = ax + b / x( 독립 변수 : 영향을 주는 변수) , y ( 종속 변수 : 영향을 받는 변수 )
- 원인을 일으키는 x변수와 결과를 보여주는 y 변수의 관계
- 모든 데이터들은 선형성을 띈다.
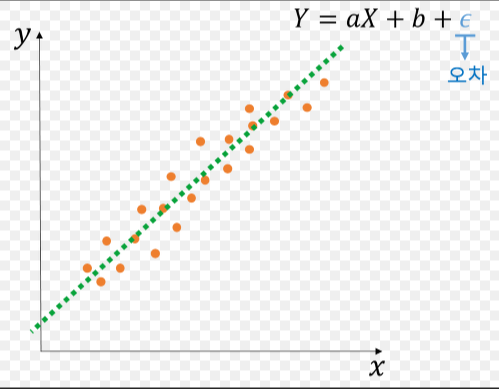
y = ax + b : 입력받은 x와 y 값을 가지고 오차를 최소화하는 a와 b의 값 찾는 과정
회귀분석의 역사 - 평균으로의 회귀
회귀분석(regression analysis)은 생물학자 프랜시스 골턴(Francis Galton)이 '평균으로의 회귀'(regression to the mean / regression towards mediocrity) 현상을 증명하기 위해 만든 것으로 알려져 있다. '평균으로의 회귀'는 부모와 아이의 키를 측정했을 때 쉽게 상상할 수 없는 극단적인 값이 되어도, 그 다음에 새로 측정을 했을 때에는 평균에 더 가까워지는 (평균으로 회귀하는) 경향성을 보고 골턴이 일반화하기 위해서 쓴 용어다.
골턴은 부모와 그 자식의 키에 대한 자료를 만들어 205명의 부모와 그들의 자식 930명의 키에 대한 자료를 분석하여 회귀계수가 2/3임을 밝혔다. 가우스의 최소제곱법을 쓰지 않고 타원으로 적합시켜 회귀계수가 2/3임을 찾아낸 것이 특이하다. 즉, 키는 유전적인 요소가 강력하게 작용한다는 것을 밝힌 것이다. 골턴은 산점도에 최초로 선형식을 표현하여 오늘날의 회귀분석을 성립하는 데 지대한 공을 세웠다.
현대에 와서는 회귀(regress), 즉 평균으로 돌아간다는 의미는 거의 사라졌다. 요즘에는 독립변수와 종속변수를 설정 [1]하고 이들의 관계를 통계적으로 살펴보는 대부분의 방법론을 다 회귀분석이라고 부르기도 한다. 시계열 데이터를 사용하면 시계열 회귀분석이고 패널 자료를 사용하면 패널 회귀 분석인 식이다.
회귀 분석 - 나무위키
이 저작물은 CC BY-NC-SA 2.0 KR에 따라 이용할 수 있습니다. (단, 라이선스가 명시된 일부 문서 및 삽화 제외) 기여하신 문서의 저작권은 각 기여자에게 있으며, 각 기여자는 기여하신 부분의 저작권�
namu.wiki
특징)
- 변수들 사이의 인과관계를 규명하고자 하는 분석방법이기 때문에 변수의 역할설정이 중요합니다.
(주의)
신문을 보는 시간이 TV를 시청하는 시간에 어떤 영향을 미치는가?’라는 물음에서 ‘신문을 보는 시간’은 원인변수에 해당하고 ‘TV를 시청하는 시간’은 결과변수입니다. 이를 뒤바꾸어 ‘TV를 시청하는 시간’을 원인변수 로 하고 ‘신문을 보는 시간’을 결과변수로 한다면 원래 의도했던 연구목적에 위배되는 것입니다.
특정 변수(독립변수)가 다른 변수(종속변수)에 어떠한 영향을 미치는가 (인과관계 분석)
예) 가격은 제품 만족도에 영향을 미치는가?
- 한 변수의 값으로 다른 변수의 값 예언
인과관계(因果關係) : 변수A가 변수B의 값이 변하는 원인이 되는 관계(변수A : 독립변수, 변수B : 종속변수)
- 회귀 방정식(Y=a+βX → Y:종속변수, a:상수, β:회귀계수, X:독립변수)을 도출하여 회귀선 추정
선형 회귀 방정식(1차 함수) : 회귀선 추정
회귀계수(β) : 단위시간에 따라 변하는 양(기울기)이며, 회귀선을 추정함에 있어 최소자승법 이용
Y= a + b*X (Y : 종속변수, a : 절편, b : 기울기, X : 독립변수)
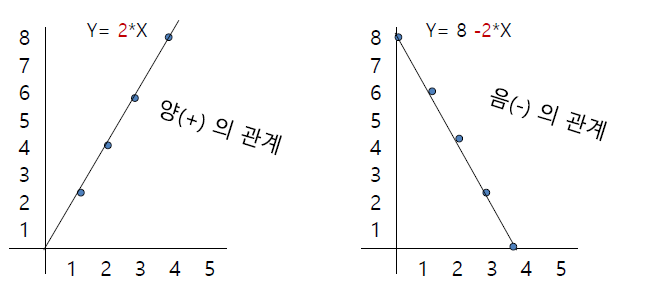
회귀방정식에 의해서 x가 10일 때 y는 20 예측 -> 회귀분석은 수치 예측
- 최소자승법 적용 회귀선
: 회귀방정식에 의해서 그려진 y의 추세선, 산포도 각 점의 위치를 기준으로 정중앙 통과하는 회귀선 추정 방법
- 산포도에 위치한 각 점에서 회귀선에 수직으로 이르는 값의 제곱의 합 최소가 되는 선(정중앙을 통과하는 직선)을
최적의 회귀선으로 추정
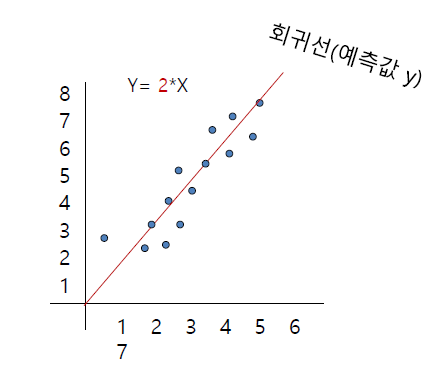
- 독립변수와 종속변수가 모두 등간척도 또는 비율척도 구성
- 상관 관계 분석 : 변수 간의 관련성 분석
- 회귀 분석 : 변수 간의 인과관계 분석
- 회귀분석의 기본 가정 충족
① 선형성 : 독립변수와 종속변수가 선형적 이어야한다. (회귀선 확인)
② 오차(잔차)의 정규성 : 오차(잔차) 란 종속변수의 관측값과 예측값 간의 차이를 말하며, 오차(잔차)의 기대값은 0이며,
정규분포를 이루어야한다. (정규성 검정 확인)
③ 오차의 독립성 : 오차들은 서로 독립적 이어야한다. (더빈-왓슨 값 확인)
④ 오차의 등분산성 : 오차들의 분산이 일정해야한다. (표준잔차와 표준예측치 도표)
⑤ 다중공선성 : 다중 회귀분석을 수행할 경우 3개 이상의 독립변수들 간의 강한 상관관계로 인한 문제가 발생되지
않아야 한다.(분산팽창요인(VIF) 확인)
- 입력으로 사용되어지는 독립변수의 독립성이 상호의존성이 높을 때 회기 분석의 결과를
신뢰할 수 없는 피드백이 나온다.
회귀모형의 형태
1) 단순(단일) 회귀 분석(Simple Regression Analysis) : 하나의 종속변수에 대해 독립변수가 하나인 경우
2) 다중 회귀 분석(Multiple Regression Analysis) : 하나의 종속변수에 대해 독립변수가 둘 이상인 경우
3) 로지스틱 회귀분석(Logistic Regression) : 분류 분석, 독립변수 -> 종속변수(분류)
회귀분석을 통해 알 수 있는 것
1) 종속변수와 독립변수 간에 선형관계가 존재하는지 알 수 있습니다.
2) 종속변수에 영향을 미치는 독립변수가 유의 한지와 영향력의 정도를 알 수 있습니다.
3) 추정된 회귀모형을 통해 종속변수의 예측치를 알 수 있습니다.
*경사하강법 : 실체 관찰치 값과 예측 값 사이의 값의 오차 = (관측치 - 예측값 = 잔차(제곱하여 음수 제거)) , 그 값의 최소의 값을 찾는 것 = 경사하강법(2차 함수 형태 = 최소값 기울기 0일 때)
① 단순(단일) 회귀 분석(Simple Regression Analysis)
– 독립변수와 종속변수 각각 1개
– 독립변수(원인 제공자)가 종속변수(영향을 받는 자)에 미치는 인과관계 분석
< 연구 가설 >
- 연구가설(H1) : 음료수 제품의 당도와 가격수준을 결정하는 제품 적절성(독립변수)은 제품 만족도(종속변수)에 정(正)의 영향을 미친다.
- 귀무가설(H0) : 음료수 제품의 당도와 가격수준을 결정하는 제품 적절성은 제품의 만족도에 영향을 미치지 않는다.
연구모델 : 제품 적절성(독립변수) -> 제품 만족도(종속변수)
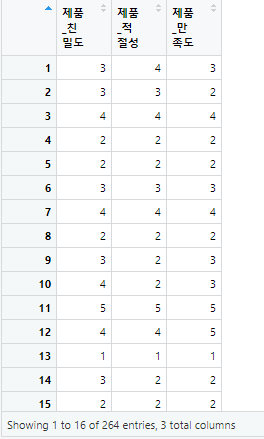
위의 데이터를 통해서 살펴보도록 하겠습니다.
- 데이터 전처리 (data.frame 데이터 생성)
str(product) # 'data.frame': 264 obs. of 3 variables:
- 출력값 -
'data.frame': 264 obs. of 3 variables:
$ 제품_친밀도: int 3 3 4 2 2 3 4 2 3 4 ...
$ 제품_적절성: int 4 3 4 2 2 3 4 2 2 2 ...
$ 제품_만족도: int 3 2 4 2 2 3 4 2 3 3 ...
y = product$제품_만족도 # 종속변수
x = product$제품_적절성 # 독립변수
df <- data.frame(x, y)
- 출력값 -
x y
1 4 3
2 3 2
3 4 4
4 2 2
5 2 2
6 3 3
- 회귀모델 생성
result.lm <- lm(formula=y ~ x, data=df)
#lm(leaning machine) = lm ( formuly= 종속변수 ~ 독립변수 , data = 데이타 셋 )
result.lm # 회귀계수 ( 절편과 기울기 ) lm : 회귀 모델 생성 ( * 알고리즘 관련 함수 저장 pakage = stats )
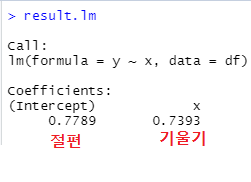
오차가 최소가 되어지는 값을 lm 을 통해서 출력준 값입니다.
- 오차를 최소화 해주는 기울기 : 0.7393 , 절편 : 0.7789
결과 : y = 0.7393x + 0.7789
- 모델의 적합값과 잔차 보기
names(result.lm)
- 출력값 -
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign"
[7] "qr" "df.residual" "xlevels" "call" "terms" "model"
fitted.values(result.lm)[1:2]
- 출력값 -
1 2
3.735963 2.996687
head(df, 1)
- 출력값 -
x y
1 4 3
Y = 0.7789 + 0.7393 * 4
Y 출력값 : 3.7361 - 회귀방정식에 의해서 계산된 적합값
# 오차(잔차:error) = Y관측값 - Y적합값
3-3.735963 출력값 : -0.735963
residuals(result.lm)[1:2] # 모델의 잔차 출력
- 출력값 -
1 2
-0.7359630 -0.9966869
-0.7359630 + 3.735963 출력값 : 3 # 잔차 + 적합값 = 관측값
- 선형회귀분석 모델 시각화[오류 확인]
① x, y 산점도 그리기
x11()
plot(formula=y ~ x, data=df)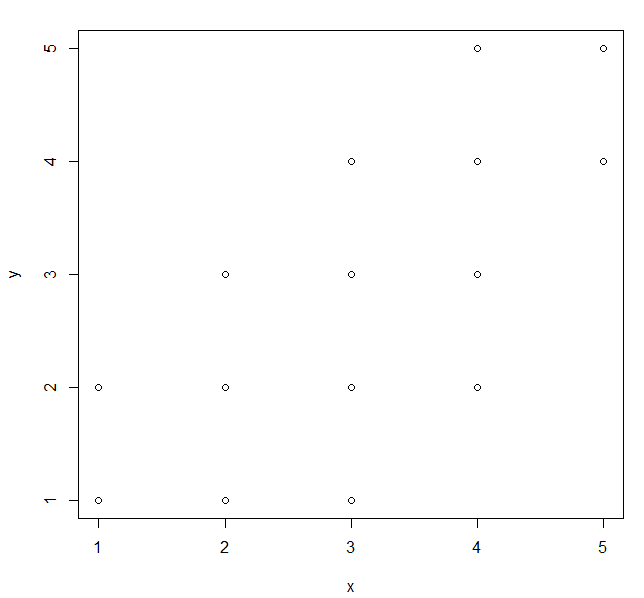
② 회귀분석 + 회귀선
result.lm <- lm(formula=y ~ x, data=df)
abline(result.lm, col='red') # 회귀선 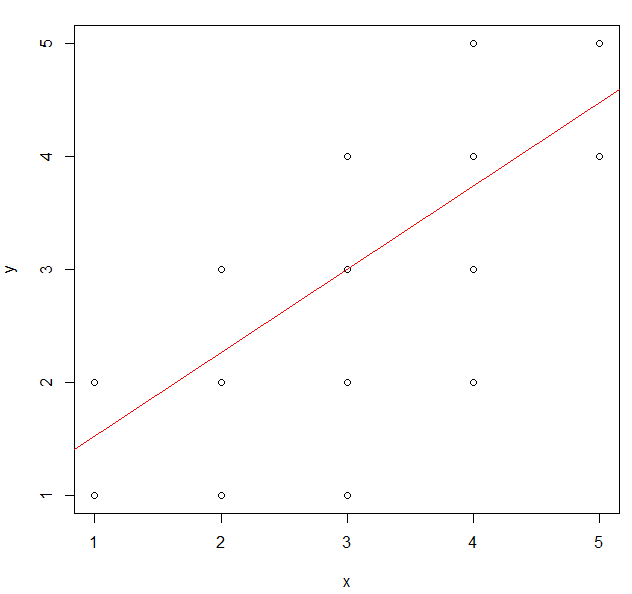
- 선형회귀 분석 결과 보기
summary(result.lm)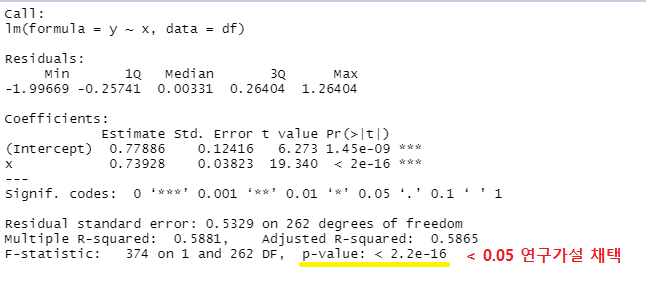
<회귀분석 결과 해석>
결정계수(Coefficients) : R-squared -> 0 ~ 1 사이의 값을 갖는다.
Multiple R-squared: 0.5881: 독립변수에 의해서 종속변수가 얼마만큼 설명되었는가?
설명력 -> 상관(결정)계수 : 58.8% 설명력
1에 가까울 수록 설명변수(독립변수)가 설명을 잘한다고 판단
모형의 변수 선정이 우수하다는 의미.
Adjusted R-squared: 0.5865 : 조정된 R값(오차를 감안한 값)<- 이것으로 분석
최종 결론 : 제품 적절성은 제품 만족도에 정(正)의 영향을 미친다.
② 다중 회귀 분석(Multiple Regression Analysis)
: 여러 개 독립변수가 1개의 종속변수에 미치는 영향 분석
< 연구 가설 >
연구가설1(H1) : 음료수 제품의 적절성(독립변수1)은 제품 만족도(종속변수)에 정(正)의 영향을 미친다.
연구가설2(H1) : 음료수 제품의 친밀도(독립변수2)는 제품 만족도(종속변수)에 정(正)의 영향을 미친다.
연구모델 : 제품 적절성(x1), 제품 친밀도(x2) -> 제품 만족도(y)

위의 데이터를 활용하여 살펴보도록 하겠습니다.
- 데이터 전처리 ( 적절성 + 친밀도 -> 만족도 )
y = product$제품_만족도 # 종속변수
x1 = product$제품_친밀도 # 독립변수2
x2 = product$제품_적절성 # 독립변수1
df <- data.frame(x1, x2, y)
head(df)
- 출력값 -
> head(df)
x1 x2 y
1 3 4 3
2 3 3 2
3 4 4 4
4 2 2 2
5 2 2 2
6 3 3 3
result.lm <- lm(formula=y ~ x1 + x2, data=df) # (+) 사용하여 추가
lm(formula=종속변수 ~ 독립변수1 + 독립변수2, data=데이터 셋)
result.lm
(잔차가 최저가 되는 기울기)결과 : y = 0.09593 * x1 + 0.68522 * x2 + 0.66731; ( y = ax1 +bx2 +c )
- 다중공선성 문제 체크
(입력으로 사용되어지는 독립변수의 독립성이 상호의존성이 높을 때 회기 분석의 결과를 신뢰할 수 없는 피드백이 나온다. )
install.packages("car")
library(car)
vif(result.lm) # x1, x2 < 10 미만인지 체크.
- 출력값 -
x1 x2
1.331929 1.331929 vif (car 패키지에서 제공하는 함수) : 입력으로 전달된 데이터 셋의 다중공선성의 문제가 발생하는지 발생하지 않는지
결과를 체크 할 수 있도록 합니다.
vif < 10미만은 독립적인 관계를 가지고 간다. ( 1.331929 , 1.331929 < 10 )
- 다중회귀 분석 결과 보기
summary(result.lm)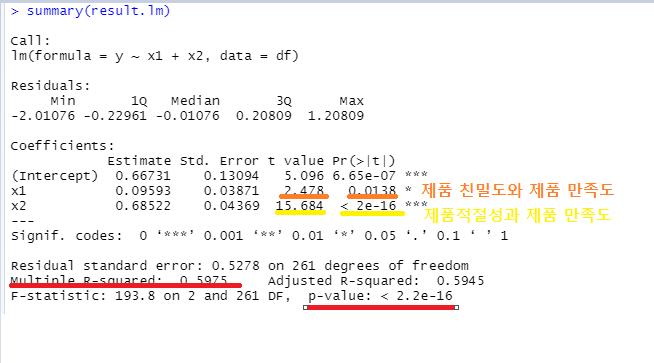
t=15.684, p < 2e-16으로 유의수준 하에서 연구가설1이 채택되었으며, 제품 친밀도가 제품 만족도에 미치는 영향은 t=2.478, p=0.0138로 유의수준하에서 연구가설2가 채택되었습니다.
Multiple R-squared: 0.5975: 독립변수에 의해서 종속변수가 얼마만큼 설명되었는가?
설명력 -> 상관(결정)계수 : 59.7% 설명력, 1에 가까울 수록 설명변수(독립변수)가 설명을 잘한다고 판단할 수 있습니다.
(모형의 변수 선정이 우수)
최종 결과 : 유의수준 0.05에서 연구가설이 채택되었다. 따라서 제품 적절성과 제품 친밀도가 높을 수록 제품 만족도가 높아지는 경향을 보이고 있다.
- 다중공선성 문제 해결과 모델 성능평가
iris 데이터를 사용하여 살펴보겠습니다.
iris
R에서 제공되는 기본 데이터 셋으로 3가지 꽃의 종류별로 50개씩 전체 150개의 관측치로 구성된다. iris는 붓꽃에 관한 데이터를 5개의 변수로 제공하며, 각 변수의 내용은 다음과 같다.
Sepal.Length(꽃받침 길이)
Sepal.Width(꽃바침 너비)
Petal.Length(꽃잎 길이)
Petal.Wodth(꽃잎 너비)
Species(꽃의 종류) : 3가지 종류별 50개(전체 150개 관측치)
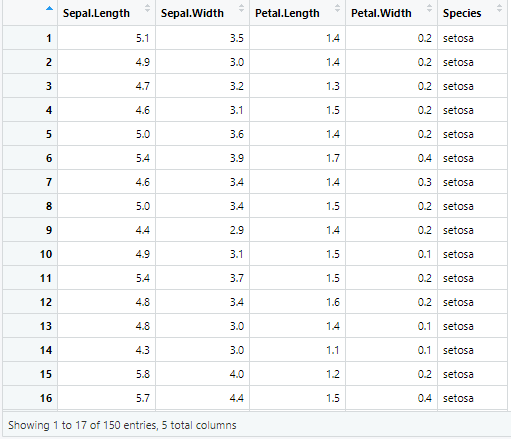
실습 ① 다중공선성 문제 확인
- iris 데이터 셋으로 다중회귀분석
fit <- lm(formula=Sepal.Length ~ Sepal.Width+Petal.Length+Petal.Width, data=iris)
vif(fit)
- 출력값 -
Sepal.Width Petal.Length Petal.Width
1.270815 15.097572 14.234335
sqrt(vif(fit))>2 # root(VIF)가 2 이상인 것은 다중공선성 문제 의심
- 출력값 -
Sepal.Width Petal.Length Petal.Width
FALSE TRUE TRUE
- iris 변수 간의 상관계수 구하기
cor(iris[,-5]) # 변수간의 상관계수 보기(Species 제외)
- 출력값 -
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000x변수들끼리 계수값이 높을 수도 있다. -> 해당 변수 제거(모형 수정) <- Petal.width
실습 ② 데이터 셋 생성과 회귀모델 생성
- 학습데이터와 검정데이터 분류
x <- sample(1:nrow(iris), 0.7*nrow(iris)) # 전체중 70%만 추출 (1~150개 중에서 70%만 랜덤으로 출력)
train <- iris[x, ] # 학습데이터 추출(70%)
test <- iris[-x, ] # 검정데이터 추출(30%)
- 변수 제거 및 다중회귀분석 - Petal.width 변수를 제거한 후 회귀 분석 ( 학습데이터 이용 모델 생성 )
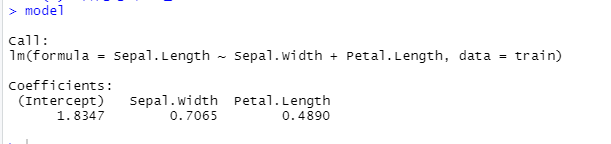
model <- lm(formula=Sepal.Length ~ Sepal.Width + Petal.Length, data=train)
- 회귀방정식 도출
model
head(train, 1)
- 출력값 -
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
70 5.6 2.5 3.9 1.1 versicolor
Y = 1.8347 + 0.7065 * 2.5 + 0.4890 * 3.9
Y 출력값 : 5.50805
- 예측치 생성 - predict()함수
pred <- predict(model, test) # x변수만 test에서 찾아서 값 예측
pred # test 데이터 셋의 y 예측치(회귀방정식 적용)
test$Sepal.Length # test 데이터 셋의 y 관측치
length(pred) 출력값 : 45 (개 벡터)

- 회귀모델 평가
cor(pred, test$Sepal.Length) 출력값 : 0.9346613
summary(pred); summary(test$Sepal.Length)
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.095 5.068 6.133 5.966 6.687 7.796
Min. 1st Qu. Median Mean 3rd Qu. Max.
4.500 5.100 6.100 6.002 6.700 7.700
③ 로지스틱 회귀분석(Logistic Regression) - 분류 분석
목적 : 일반 회귀분석과 동일하게 종속변수와 독립변수 간의 관계를 나타내어 향후 예측 모델을 생성하는데 있습니다.
차이점 : 종속변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나눠지기 때문에 분류분석 방법으로 분류됩니다.
(종속변수(y)를 범주군으로 분류군으로 결과가 피드백 되어지는 분석법)
유형 : 이항형(종속변수가 2개 범주-Yes/No), 다항형(종속변수가 3개 이상 범주-iris 꽃 종류)
다항형 로지스틱 회귀분석 : nnet, rpart 패키지 이용
a : 0.6, b:0.3, c:0.1 -> a 분류
분야 : 의료, 통신, 기타 데이터마이닝
- 결과는 0이 아니면 1의 값으로, 두가지 분류군으로 구분지어서 어느 영역에 해당되는지 출력합니다.
선형회귀분석 vs 로지스틱 회귀분석
1. 로지스틱 회귀분석 결과는 0과 1로 나타난다.(이항형)
2. 정규분포(연속형) 대신에 이항분포(범주형)를 따른다.
3. 로직스틱 모형 적용 : 변수[-무한대, +무한대] -> 변수[0,1]사이에 있도록 하는 모형
-> 로짓변환 : 출력범위를 [0,1]로 조정
4. 종속변수가 2개 이상인 경우 더미 변수(dummy variable)로 변환하여 0과 1를 갖도록한다.
예) 혈액형 A인 경우 -> [1,0,0,0] AB(1) -> A,B,O(0)
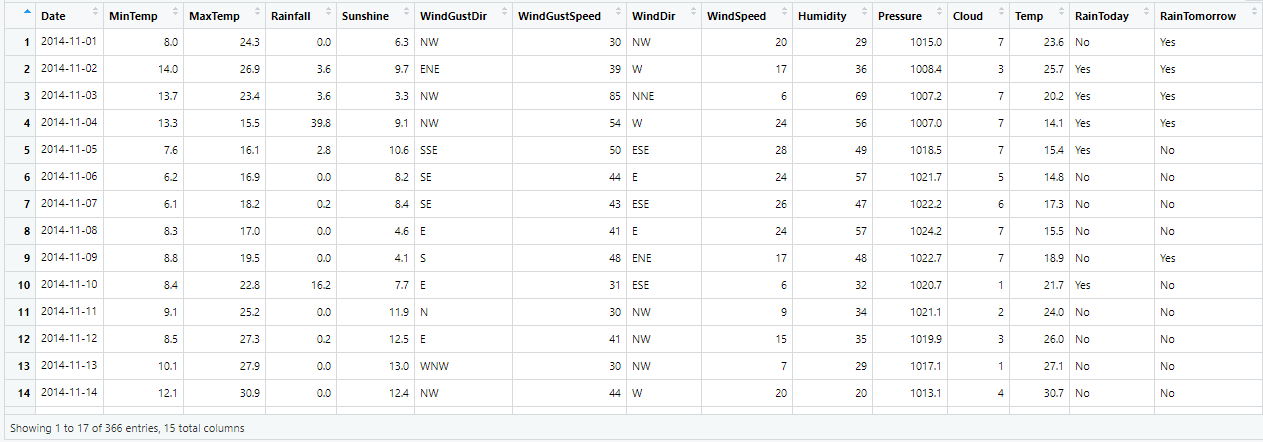
위의 데이터를 활용하여 살펴보도록 하겠습니다.
- 데이터 확인
dim(weather) 출력값 : 366 15
str(weather)
- 출력값 -
data.frame': 366 obs. of 15 variables:
$ Date : chr "2014-11-01" "2014-11-02" "2014-11-03" "2014-11-04" ...
$ MinTemp : num 8 14 13.7 13.3 7.6 6.2 6.1 8.3 8.8 8.4 ...
$ MaxTemp : num 24.3 26.9 23.4 15.5 16.1 16.9 18.2 17 19.5 22.8 ...
$ Rainfall : num 0 3.6 3.6 39.8 2.8 0 0.2 0 0 16.2 ...
$ Sunshine : num 6.3 9.7 3.3 9.1 10.6 8.2 8.4 4.6 4.1 7.7 ...
$ WindGustDir : chr "NW" "ENE" "NW" "NW" ...
$ WindGustSpeed: int 30 39 85 54 50 44 43 41 48 31 ...
$ WindDir : chr "NW" "W" "NNE" "W" ...
$ WindSpeed : int 20 17 6 24 28 24 26 24 17 6 ...
$ Humidity : int 29 36 69 56 49 57 47 57 48 32 ...
$ Pressure : num 1015 1008 1007 1007 1018 ...
$ Cloud : int 7 3 7 7 7 5 6 7 7 1 ...
$ Temp : num 23.6 25.7 20.2 14.1 15.4 14.8 17.3 15.5 18.9 21.7 ...
$ RainToday : chr "No" "Yes" "Yes" "Yes" ...
$ RainTomorrow : chr "Yes" "Yes" "Yes" "Yes" ...
head(weather)
- 데이터 전처리
Date, RainToday 칼럼 제거
weather_df <- weather[, c(-1, -6, -8, -14)]
str(weather_df)
- 출력값 -
str(weather_df)
'data.frame': 366 obs. of 11 variables:
$ MinTemp : num 8 14 13.7 13.3 7.6 6.2 6.1 8.3 8.8 8.4 ...
$ MaxTemp : num 24.3 26.9 23.4 15.5 16.1 16.9 18.2 17 19.5 22.8 ...
$ Rainfall : num 0 3.6 3.6 39.8 2.8 0 0.2 0 0 16.2 ...
$ Sunshine : num 6.3 9.7 3.3 9.1 10.6 8.2 8.4 4.6 4.1 7.7 ...
$ WindGustSpeed: int 30 39 85 54 50 44 43 41 48 31 ...
$ WindSpeed : int 20 17 6 24 28 24 26 24 17 6 ...
$ Humidity : int 29 36 69 56 49 57 47 57 48 32 ...
$ Pressure : num 1015 1008 1007 1007 1018 ...
$ Cloud : int 7 3 7 7 7 5 6 7 7 1 ...
$ Temp : num 23.6 25.7 20.2 14.1 15.4 14.8 17.3 15.5 18.9 21.7 ...
$ RainTomorrow : chr "Yes" "Yes" "Yes" "Yes" ...
RainTomorrow 칼럼 -> 로지스틱 회귀분석 결과(0,1)에 맞게 더미변수 생성
weather_df$RainTomorrow[weather_df$RainTomorrow=='Yes'] <- 1
weather_df$RainTomorrow[weather_df$RainTomorrow=='No'] <- 0
weather_df$RainTomorrow <- as.numeric(weather_df$RainTomorrow)
str(weather_df)
- 출력값 -
'data.frame': 366 obs. of 11 variables:
$ MinTemp : num 8 14 13.7 13.3 7.6 6.2 6.1 8.3 8.8 8.4 ...
$ MaxTemp : num 24.3 26.9 23.4 15.5 16.1 16.9 18.2 17 19.5 22.8 ...
$ Rainfall : num 0 3.6 3.6 39.8 2.8 0 0.2 0 0 16.2 ...
$ Sunshine : num 6.3 9.7 3.3 9.1 10.6 8.2 8.4 4.6 4.1 7.7 ...
$ WindGustSpeed: int 30 39 85 54 50 44 43 41 48 31 ...
$ WindSpeed : int 20 17 6 24 28 24 26 24 17 6 ...
$ Humidity : int 29 36 69 56 49 57 47 57 48 32 ...
$ Pressure : num 1015 1008 1007 1007 1018 ...
$ Cloud : int 7 3 7 7 7 5 6 7 7 1 ...
$ Temp : num 23.6 25.7 20.2 14.1 15.4 14.8 17.3 15.5 18.9 21.7 ...
$ RainTomorrow : chr "Yes" "Yes" "Yes" "Yes" ...
View(weather_df) # head(weather_df) 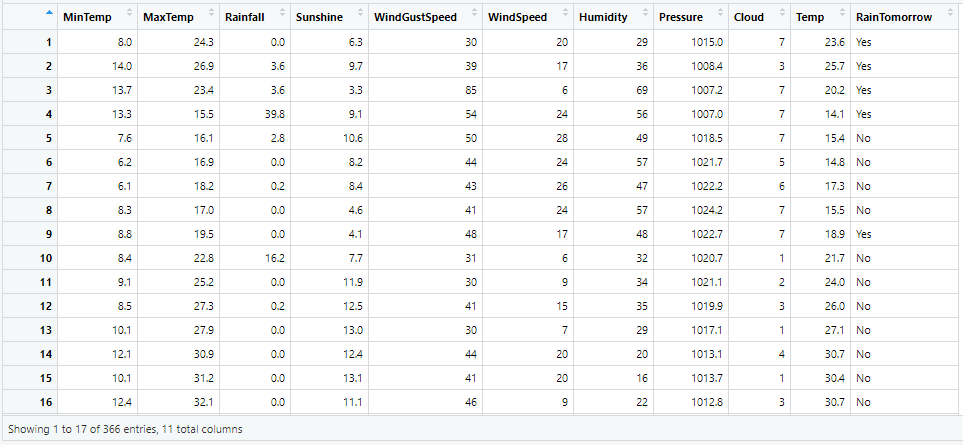
- 로지스틱 회귀분석(Logistic Regression) -> 7:3 비율
idx <- sample(1:nrow(weather_df), nrow(weather_df)*0.7) # 랜덤으로 70% 출력
train <- weather_df[idx, ] # 70%
test <- weather_df[-idx, ] # 30%
- 로지스틱 회귀모델 생성 : 학습데이터
weater_model <- glm(RainTomorrow ~ ., data = train, family = 'binomial')
weater_model
summary(weater_model) 
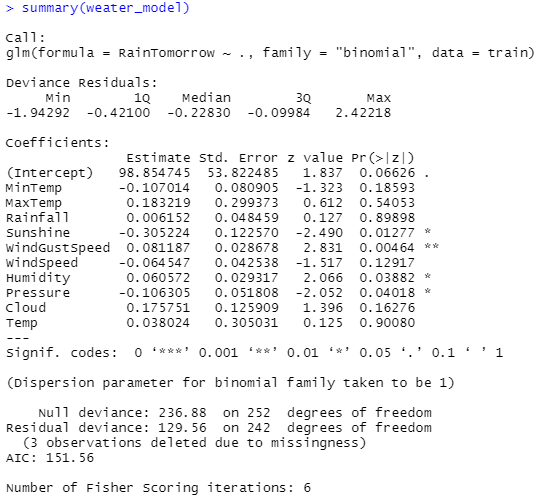
- 로지스틱 회귀모델 예측치 생성
newdata=test : 새로운 데이터 셋, type="response" : 0~1 확률값으로 예측
pred <- predict(weater_model, newdata=test, type="response")
pred
summary(pred)
- 출력값 -
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.001244 0.019221 0.081876 0.225368 0.385520 0.975289 2
str(pred)
- 출력값 -
Named num [1:110] 0.1094 0.0109 0.0193 0.0502 0.0594 ...
- attr(*, "names")= chr [1:110] "2" "11" "15" "19" ...

- 예측치 : 0과 1로 변환(0.5)
result_pred <- ifelse(pred >= 0.5, 1, 0) # 비가올 활률 50% 이상 : 1, 비가올 활률 50% 이하 : 0
result_pred
table(result_pred)
- 출력값 -
result_pred 0 1
0 86 11
1 1 10

- 모델 평가 : 분류정확도
table(result_pred, test$RainTomorrow)
- 출력값 -
result_pred 0 1
0 86 11
1 1 10
모델의 분류정확도
(80+13) / (86+11+1+10) # 0.8611111 = 86.11%
- ROC(Receiver Operating Characteristic) Curve를 이용한 모델 평가
install.packages("ROCR")
library(ROCR)
- ROCR 패키지 제공 함수 : prediction() -> performance
pr <- prediction(pred, test$RainTomorrow)
pr
-출력값-
A prediction instance
with 110 data points
prf <- performance(pr, measure = "tpr", x.measure = "fpr")
plot(prf)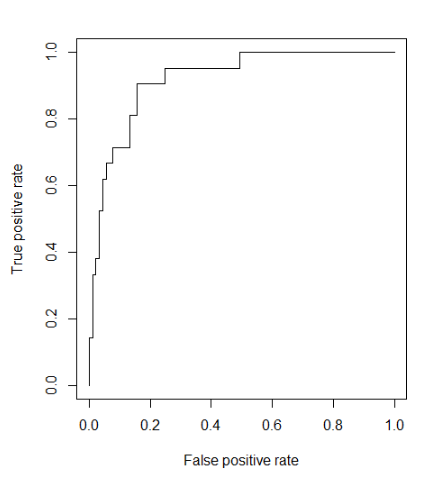
'빅데이터 > R' 카테고리의 다른 글
| [R] 비지도 학습의 방법 : 군집분석(Clustering Analysis) (0) | 2020.07.21 |
|---|---|
| [R] 지도학습의 방법 : 분류분석(Classification) (0) | 2020.07.20 |
| [R] 머신러닝(Machine Learning) (0) | 2020.07.17 |
| [R] 상관관계 분석(Correlation Analysis) (0) | 2020.07.17 |
| [R] 요인분석(Factor Analysis) (1) | 2020.07.16 |




